Aufgabe 1 Zeige, dass für das Volumen V und die Oberfläche O gilt:
V = 1 6 π d 3 ; O = π d 2
Lösung
Volumen V :
V = 4 3 · π · r 3 | r = d 2 einsetzen
V = 4 3 · π · ( d 2 ) 3 = 4 3 · π · d 8 3 = 4 3 · 8 π d 3
Oberfläche O :
O = 4 · π · r 2 | r = d 2 einsetzen
O = 4 · π · ( d 2 ) 2 = 4 · π · d 4 2 = 4 4 · π · d 2 = π d 2
Aufgabe 2 Berechne die in der Tabelle jeweils fehlenden Größen der Kugel. Runde die Ergebnisse sinnvoll.
a) b) c) d) e) Radius r 4 mm Durchmesser d 12 cm Oberfläche O 36π dm² Volumen V 4,5π m³ 113,1 l
Lösung
V = 4 3 · π · r 3 = 1 6 · π · d 3 ; d = 6 · V π 3
O = 4 · π · r 2 = π · d 2 ; d = O π
a) b) c) d) e) Radius r 4 mm 6 cm 3 dm 1,5 m 3 dm Durchmesser d 8 mm 12 cm 6 dm 3 m 6 dm Oberfläche O 201,1 mm² 452,4 cm² 36π dm² 28,3 m² 28 ,27 dm² Volumen V 268,1 mm³ 904,8 cm³ 113,1 dm³ 4,5π m³ 113,1 l
Aufgabe 3 In Omas Schmuckkästchen findest du eine goldig glänzende Kugel und fragst dich, wie wertvoll sie ist.
Du weißt, dass die Dichte ρ von Gold 19,3 g cm 3 beträgt und mit der Formel ρ = m V berechnet wird.
Beim Wiegen der Kugel zeigt die Waage eine Masse von 70,7 g und beim Messen des Durchmessers zeigt das Messgerät 2,58 cm an.
Ist die Kugel aus Gold oder nicht?
Lösung
Ermittlung des Kugelvolumens V :
V = 1 6 · π · d 3 = 1 6 · π · 2,58 3 ≈ 9 [ cm 3 ]
Ermittlung der Dichte ρ :
ρ = m V = 70,7 g 9 cm 3 = 7,85 g cm 3
Es handelt sich leider um keine Goldkugel, sondern um eine vergoldete Kugel.
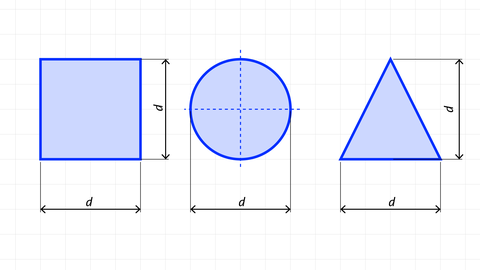
Aufgabe 4 Vergleiche die Volumen von Zylinder, Kugel und Kegel bei gleichem Durchmesser d und gleicher Höhe h mit h = d und gib deren Volumenverhältnisse an."Volumen und Oberfläche von Pyramide und Kegel" und "Volumen und Oberfläche von Prisma und Zylinder" .)
BR
Lösung
In die Formel für r = d 2 und für h = d einsetzen
Volumen Zylinder:
V Zy = π · r 2 · h = π · ( d 2 ) 2 · d = π 4 · d 3
Volumen Kugel:
V Ku = 4 3 · π · r 3 = 4 3 · π · ( d 2 ) 3 = 4 3 · π · d 8 3 = 4 3 · 8 · π · d 3 = π 6 · d 3
Volumen Kegel:
V Ke = 1 3 · π · r 2 · h = 1 3 · π · ( d 2 ) 2 · d
= 1 3 · π · d 4 2 · d = 1 3 · π · d 4 2 · d = π 12 · d 3
Verhältnis bilden (Nenner gleichnamig machen):
V Zy : V Ku : V Ke = π 12 · 3 d 3 : π 12 · 2 d 3 : π 12 · d 3 = 3 : 2 : 1
Aufgabe 5 Als du deine Fahrradkette ölst, fällt ein Tropfen zu Boden. Wegen der Kohäsionskräfte bildet der Tropfen beim Runterfallen eine Kugelform mit einem Durchmesser d = 2 mm. Am Boden angekommen bildet das Öl eine kreisrunde Fläche von 0,5 m². Bestimme die Höhe h dieses Ölfilms.
Lösung
Volumen des Öltropfens:
V Ö = 1 6 · π · d 3 = 1 6 · π · 2 3 ≈ 4,19 [ mm 3 ]
Der Ölfleck am Boden hat die Form eines Zylinders, bei dem die Höhe h zu bestimmen ist.
Volumen des Zylinders:
V Z = V Ö = 4,19 [ mm 3 ]
Bestimmung der Höhe h des Ölfilms:
V Z = A G · h | : A G mit A G = 0,5 [ m 2 ]
h = V Z A G = 4,19 5000 = 8,38 · 10 − 6
Aufgabe 6 Bauschutt wird über ein Förderband aufgeschüttet, insgesamt 620 m³ Material. Der Kegel hat eine Höhe von 8 Metern. Bestimme den Inhalt der Bodenfläche G des Schuttkegels.
Adobe Stock
adobe.stock/Rattanapon
Lösung
Zur Bestimmung der Bodenfläche G wird der Radius r benötigt.
V = 4 3 · π · r 3 | · 3 4 · π
⇒ r = 3 · V 4 · π 3 = 3 · 620 4 · π 3 ≈ 5,29 [ m ]
Bodenfläche G :
G = π · r 2 = π · 5,29 2 = 87,9 [ m 2 ]
Aufgabe 7 Bestimme den Durchmesser d einer Kugel so, dass die Maßzahl des Volumens V der Maßzahl der Oberfläche O entspricht.
Lösung
Wenn die Maßzahlen von Volumen und Oberfläche gleich sein sollen, dann werden die Formeln von Volumen und Oberfläche gleichgesetzt.
V = O ⇒ 1 6 π d 3 = π d 2 | − π d 2
1 6 π d 3 − π d 2 = 0 | π d 2 ausklammern
π d 2 ( 1 6 d − 1 ) = 0 | Satz vom Nullprodukt: Ein Produkt ist null, wenn ein Faktor null ist.
Diese Lösung ist unsinnig, da bei d = 0 keine Kugel vorhanden ist.
1 6 d − 1 = 0 | + 1 | · 6 ⟹ d = 6
Für d = 6 ist die Maßzahl des Volumens der Kugel gleich der Maßzahl der Kugeloberfläche.
(Siehe auch "Spezielle quadratische Gleichungen" )
Aufgabe 8 Ein "Stehaufmännchen" besteht aus einer Halbkugel und einem Kegel. Bestimme das Volumen V der Figur, wenn die Höhe h des Kegels genauso groß ist wie der Durchmesser d der Halbkugel.
BR
Lösung
Für das Volumen V der Figur gilt: V = V Halbkugel + V Kegel
V Halbkugel = 1 2 · 1 6 · π · d 3 = π 12 · d 3
V Kegel = π · r 2 · h mit r = d 2 und h = d gilt:
V Kegel = π · ( d 2 ) 2 · d = π · d 2 4 · d = π 4 · d 3
V = π 12 · d 3 + π 4 · d 3 = ( π 12 + π 4 ) · d 3
= ( π 12 + 3 π 12 ) · d 3 = 4 π 12 · d 3 = π 3 · d 3