Volumen und Oberfläche von Pyramide und Kegel

In diesem Kapitel werden anhand von Beispielaufgaben das Volumen und die Oberfläche einer Pyramide sowie eines Kegels berechnet.

Volumen und Oberfläche einer Pyramide

Das Volumen einer Pyramide ist der Raum, den die Pyramide im dreidimensionalen Raum einnimmt. Es gibt an, wie viel Platz sie innerhalb ihrer Begrenzungen hat.

Die Oberfläche einer Pyramide ist die gesamte Fläche, die die Pyramide umschließt. Sie setzt sich aus zwei Teilen zusammen:

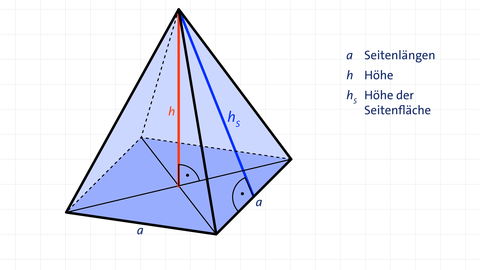
Grundfläche G – die untere Fläche der Pyramide (z. B. Quadrat, Rechteck oder Dreieck).
Mantelfläche M – die Summe der Flächen aller seitlichen Dreiecke.

Quadratische Pyramide

$Grundfläche G : G = a \cdot a = a^{2}$

$Volumen V : V = \frac{1}{3} \cdot G \cdot h = \frac{1}{3} \cdot a^{2} \cdot h$

$Mantelfläche M : M = 2 \cdot a \cdot h_{s}$

$Oberfläche O : O = a \cdot (a + 2 \cdot h_{s})$

Grafik einer quadratischen Pyramide | kolleg24 Mathematik — BR

Beispiel: Quadratische Pyramide

Ermittle das Volumen und die Oberfläche einer quadratischen Pyramide mit der Seitenlänge a = 6 cm und h = 10 cm.

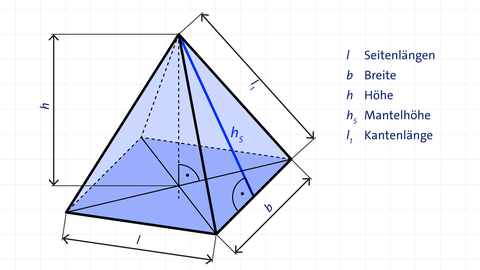
Rechteckige Pyramide

$Grundfläche G : G = l \cdot b$

$Volumen V : V = \frac{1}{3} \cdot G \cdot h = \frac{1}{3} \cdot l \cdot b \cdot h$

$Mantelfläche M : M = l \cdot h_{s} + b \cdot h_{s}$

$Oberfläche O : O = l \cdot b + l \cdot h_{s} + b \cdot h_{s}$

Grafik einer rechteckigen Pyramide | kolleg24 Mathematik — BR

Beispiel: Rechteckige Pyramide

$Eine Pyramide mit rechteckiger Grundfläche hat eine Höhe h = 9 dm, die Seitenlänge l = 8 dm und die Breite b = 6 dm.$

$Berechne das Volumen der Pyramide und die Mantelfläche, wenn h_{sl} = 10 dm (Höhe auf l) und h_{sb} = 8 dm (Höhe auf b) betragen.$

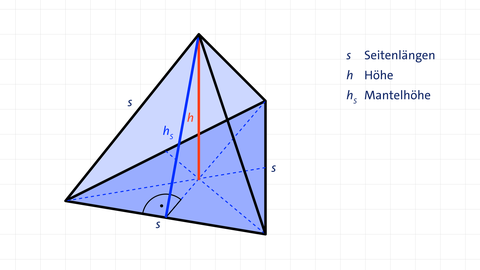
Dreieckspyramide (Tetraeder)

$Grundfläche G : G = \frac{1}{2} \cdot s \cdot h_{s}$

$Volumen V : V = \frac{1}{3} \cdot G \cdot h = \frac{1}{6} \cdot s \cdot h_{s} \cdot h$

$Mantelfläche M : M = \frac{3}{2} \cdot s \cdot h_{s}$

$Oberfläche O : O = 2 \cdot s \cdot h_{s}$

Grafik einer Dreieckspyramdie (Tetraeder) | kolleg24 Mathematik — BR

Beispiel: Tetraeder

$Eine 4 Dezimeter hohe gleichseitige Dreieckspyramide hat ein Volumen von 3 \sqrt{3} Kubikdezimeter.$

Ermittle die Oberfläche O und die Seitenlänge s des Tetraeders.

Volumen und Oberfläche eines Kegels

Das Volumen eines Kegels ist der Rauminhalt, den der Kegel im dreidimensionalen Raum einnimmt.

Die Oberfläche eines Kegels ist die gesamte Fläche, die der Kegel umschließt. Sie setzt sich aus zwei Teilen zusammen:

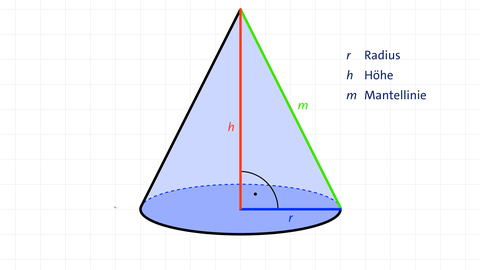
Grundfläche G: die untere (Boden-)Fläche des Kegels, ein Kreis mit dem Radius r
Mantelfläche M: ein Kreisausschnitt mit der Mantellinie s als Radius

$Grundfläche G : G = π r^{2}$

$Volumen V : V = \frac{1}{3} G \cdot h = \frac{1}{3} π r^{2} h$

$Mantelfläche M : M = π r m$

$Oberfläche O : O = G + π \cdot r \cdot m = π r (r + m)$

$Mantellinie m : m = \sqrt{r^{2} + h^{2}}$

Grafik eines Kegels | kolleg24 Mathematik — BR

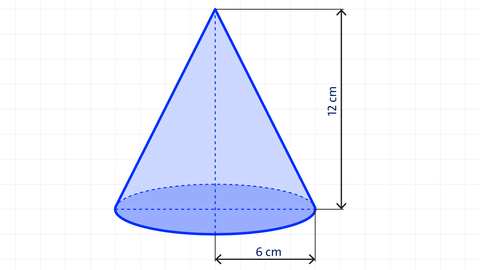
Beispiel: Kegel

Ermittle für einen Kegel, bei dem Durchmesser und Höhe die gleiche Maßzahl haben,

a) das Volumen und die Oberfläche.
b) Wie ändert sich das Volumen, wenn der Radius verdoppelt wird?

Grafik eines Kegels mit Längenmaßen | kolleg24 Mathematik — BR

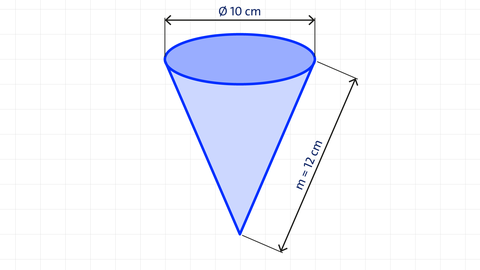
Beispiel: Filtertüte

Eine Kaffeefiltertüte hat einen Durchmesser d = 10 cm und eine Mantellinie der Länge m = 12 cm.

a) Ermittle das Fassungsvermögen der Filtertüte in cm³ und Liter, wenn sie vollständig mit Flüssigkeit gefüllt wird.
b) Bestimme die Maßzahl der Fläche des Filterpapiers in cm², wenn für die Verbindungsnaht und den Zuschnitt eine Zugabe von 10 % eingeplant ist.

Grafik einer Filtertüte mit Längenmaßen | kolleg24 Mathematik — BR