In diesem Kapitel werden anhand von Beispielaufgaben das Volumen und die Oberfläche eines Prismas sowie eines Zylinders berechnet.
Elementare Flächen- und Volumenberechnung: Volumen und Oberfläche eines Prismas
Ein Prisma ist ein geometrischer Körper mit zwei parallelen und kongruenten (deckungsgleichen) Grundflächen sowie rechteckigen bzw. quadratischen Seitenflächen.
Arten von Prismen:
Gerades Prisma:
Die Seitenkanten stehen senkrecht auf den Grundflächen.
Spezielle Prismen:
- Würfel (Spezialfall eines Prismas mit quadratischer Grundfläche und gleichen Kantenlängen)
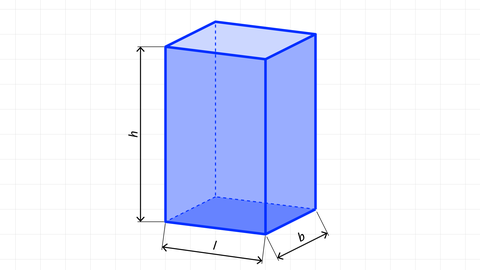
- Quader (Prisma mit rechteckiger Grundfläche)
Beispiele für Prismen aus dem Alltag und aus der Mathematik:
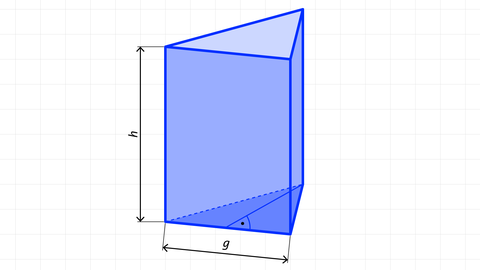
1. Dreiecksprisma
Beispiel: ein Dach mit einer dreieckigen Seitenansicht
Eigenschaft: Grundfläche ist ein Dreieck
2. Rechteckprisma (Quader)
Beispiele: Schuhkarton, Taschenbuch, Ziegelstein
Eigenschaft: Grundfläche ist ein Rechteck
3. Quadratprisma (Würfel)
Beispiele: Rubik’s Cube (Zauberwürfel), Würfel aus einem Brettspiel
Eigenschaft: alle Seitenflächen sind Quadrate
4. Sechseckprisma
Beispiel: eine Bleistiftmine in einem klassischen sechseckigen Bleistift
Eigenschaft: Grundfläche ist ein Sechseck
Volumen eines Körpers
Das Volumen eines Körpers wird in Kubikmeter m³, in Kubikdezimeter (Liter) dm³, Kubikzentimeter cm³ oder in Kubikmillimeter mm³ angegeben.
| Einheiten | Umformungen | |||
| m³ | 1 m³ = | 10³ dm³ | 10⁶ cm³ | 10⁹ mm³ |
| dm³ | 1 dm³ = | 10⁻³ m³ | 10³ cm³ | 10⁶ mm³ |
| cm³ | 1 cm³ = | 10⁻⁶ m³ | 10⁻³ dm³ | 10³ mm³ |
| mm³ | 1 mm³ = | 10⁻⁹ m³ | 10⁻⁶ dm³ | 10⁻³ cm³ |
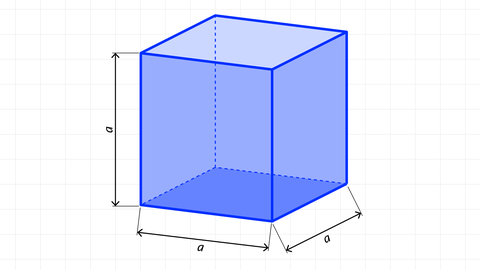
Beispielaufgabe: Würfel
Ein Rubik’s Cube (Zauberwürfel) hat die Seitenlänge a = 56 mm.
a) Berechne das Volumen V und die Oberfläche O des Würfels.
b) Der Würfel besteht aus 27 kleineren Würfeln. Ermittle das Volumen eines dieser kleinen Würfel.

Beispielaufgabe: Quader
Eine Lautsprecherbox hat eine Länge a = 32 cm, eine Breite b = 26 cm und eine Höhe h = 60 cm.
a) Berechne das Volumen V in Liter.
b) Eine Lautsprecherbox mit dem gleichen Volumen soll als Würfel hergestellt werden. Ermittle die Seitenlänge a des Würfels.
Beispielaufgabe: Dreiecksprisma
Ein Holzkeil (z.B. ein Türstopper), der senkrecht zur Grundlinie geschnitten abgesägt ist, hat eine Grundlinie g = 28 cm, eine Höhe hg = 7 cm und eine Breite b = h = 10 cm. Ermittle das Volumen und die Masse des Holzkeils, wenn 1 m³ Holz eine Masse von 870 kg hat.

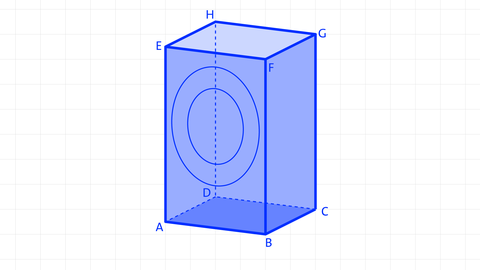
Volumen und Oberfläche eines Zylinders
Ein Zylinder ist ein Körper mit zwei parallelen Kreisflächen (Grundfläche und Deckfläche, die gleich groß sind) und einer Mantelfläche.
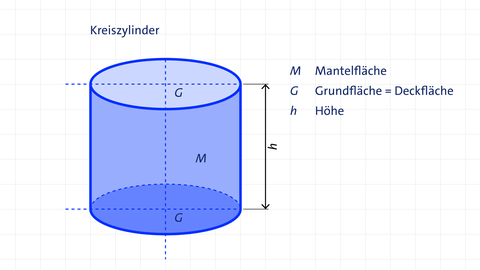
Volumen:
Das Volumen V gibt an, wie viel Raum der Zylinder innen hat.
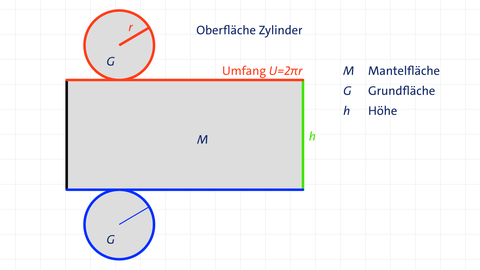
Oberfläche:
Die Oberfläche O eines Zylinders setzt sich aus zweimal der Grundfläche G und der Mantelfläche M (ein aufgerolltes Rechteck) zusammen.
Beispielaufgabe: eine mit Erbsen gefüllte Dose
Eine Konservendose mit Erbsen hat einen Durchmesser von 7 cm und eine Höhe von 8 cm. Berechne das Volumen in Milliliter und die Oberfläche der Dose in Quadratzentimeter.
Beispielaufgabe: eine mit Mais gefüllte Zylinderdose
Eine Konservendose mit Mais mit einem Volumen von 680 ml hat einen Durchmesser von 9 cm.
a) Ermittle die Höhe h und den Oberflächeninhalt O der Dose.
b) Die Dose soll mit einer Banderole umhüllt werden. Der Klebefalz ist 1,5 cm breit, der Abstand der Banderole von Boden und Deckel beträgt jeweils 2 mm. Bestimme den Flächeninhalt der Banderole.

Beispielaufgabe: Regentonne
Eine zylindrische Regentonne aus Metall hat den Innendurchmesser d = 80 cm und die Höhe h = 1m.
a) Bestimme das maximale Füllvolumen V der Regentonne in Liter.
b) Die Regentonne soll Innen gegen Rost beschichtet werden. Ermittle die Beschichtungsfläche in dm².
c) Berechne, wie hoch der Wasserspiegel ist, wenn 380 Liter Wasser in der Tonne sind.
Beispielaufgabe: Litfaßsäule
Eine 3,5 m hohe Litfaßsäule aus Beton hat einen Außendurchmesser d₂ = 1,2 m und einen Innendurchmesser d₁ = 1 m.
b) Bestimme den Flächeninhalt, der für Plakate zur Verfügung steht.