In diesem Kapitel lernst du, wie man den Umfang und den Flächeninhalt von Rechtecken, Parallelogrammen und Trapezen berechnet.
Flächeninhalt und Umfang von Vierecken
Die Fläche A eines Vierecks ist das zweidimensionale Gebilde, das von seinen vier Seiten eingeschlossen wird.
Der Umfang U eines Vierecks ist die Gesamtlänge seiner vier Seiten.
Rechteck
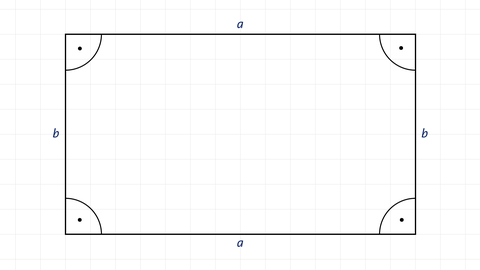
Ein Viereck, bei dem benachbarte Seiten senkrecht aufeinander stehen, heißt Rechteck. Die gegenüberliegenden Seiten sind jeweils gleich lang und parallel.
Quadrat
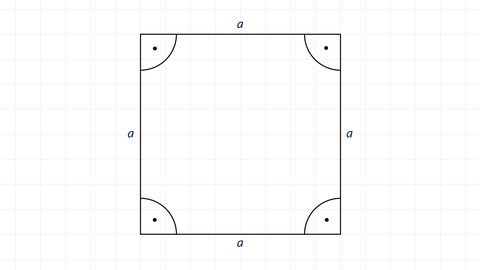
Ein Rechteck mit vier gleich langen Seiten nennt man Quadrat.
Beispielaufgabe: Flächeninhalt und Umfang eines Rechtecks
Ein Rechteck hat die Seitenlängen a = 6 m und b = 3 m.
a) Berechne den Flächeninhalt A und den Umfang U des Rechtecks.
b) Ermittle die Seitenlänge a eines Quadrats mit der gleichen Fläche.
c) Ermittle die Seitenlänge a eines Quadrats mit dem gleichen Umfang.
Parallelogramm
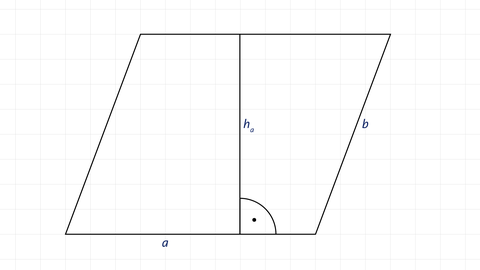
Ein Viereck, bei dem je zwei gegenüberliegende Seiten parallel sind, nennt man Parallelogramm. Die jeweils gegenüberliegenden Seiten sind gleich lang.
Trapez
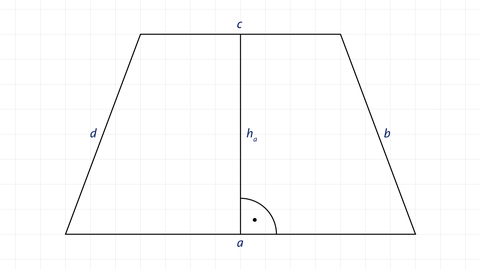
Ein Trapez ist ein Viereck, bei dem zwei gegenüberliegende Seiten parallel sind.
Beispielaufgabe: Parallelogramm
Ein Parallelogramm hat eine Basislänge a = 8 cm und eine Höhe hₐ = 5 cm.
a) Berechne den Flächeninhalt des Parallelogramms.
b) Die andere Seite des Parallelogramms hat die Länge b = 6 cm. Berechne den Umfang des Parallelogramms.
c) Die Höhe des Parallelogramms wird verdoppelt. Bestimme, wie sich der Flächeninhalt verändert.
Beispielaufgabe: Trapez
Ein Trapez hat den Flächeninhalt A = 42 cm², die Höhe hₐ = 60 mm und eine parallele Seitenlänge a = 80 mm. Bestimme die Länge der zweiten parallelen Seite c. Ermittle auch den Umfang U des Trapezes, wenn die Länge von Seite b = 61,8 mm und die von Seite d = 60,2 mm beträgt.
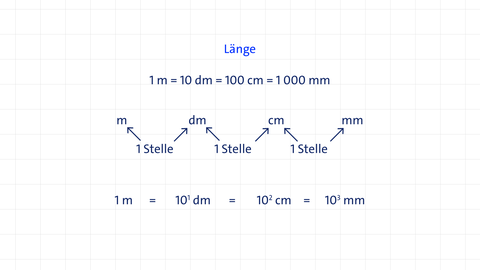
Umwandlung von Längeneinheiten
Übung zu Flächeninhalt und Umfang von Parallelogramm und Trapez