In diesem Kapitel lernst du die Trigonometrie am rechtwinkligen Dreieck kennen und erfährst, was man unter einem Einheitskreis versteht. Außerdem wirst du den Bezeichnungen der Seitenverhältnisse im rechtwinkligen Dreieck vertraut gemacht.
Die Trigonometrie am rechtwinkligen Dreieck beschäftigt sich mit den Zusammenhängen zwischen den Winkeln und Seitenlängen eines solchen Dreiecks. Dabei kommen spezielle Funktionen, die sogenannten Trigonometrischen Funktionen, zum Einsatz, um diese Beziehungen zu beschreiben und zu berechnen.
In einem rechtwinkligen Dreieck gibt es immer einen rechten Winkel (90°), die anderen beiden Winkel sind jeweils kleiner als 90°. Die Seiten des Dreiecks sind dabei in Bezug auf einen bestimmten Winkel benannt:
- Hypotenuse: die längste Seite, die dem rechten Winkel gegenüberliegt.
- Gegenkathete: die Seite, die dem betrachteten Winkel gegenüberliegt.
- Ankathete: die Seite, die den betrachteten Winkel mit dem rechten Winkel bildet.
Der Einheitskreis
Ein Einheitskreis ist ein Kreis im kartesischen Koordinatensystem, dessen Mittelpunkt im Ursprung (0|0) liegt und dessen Radius 1 ist. Das bedeutet, dass für jeden Punkt P(x|y) auf diesem Kreis die folgende Gleichung gilt:
x² + y² = 1
Der Einheitskreis dient als Grundlage für trigonometrische Funktionen wie Sinus und Kosinus und Tangens. Die Werte dieser Funktionen können durch die Koordinaten von Punkten auf dem Einheitskreis dargestellt werden.
Der trigonometrische Pythagoras
Der trigonometrische Pythagoras bezieht sich auf die Beziehung, die zwischen den trigonometrischen Funktionen Sinus, Kosinus und dem Satz des Pythagoras im Einheitskreis besteht:
x² + y² = 1² = 1
Geometrische Interpretation:
- Auf dem Einheitskreis (mit Radius 1) entspricht der Kosinus eines Winkels α der x-Koordinate und der Sinus des Winkels α der y-Koordinate eines Punktes auf dem Kreis.
- Der Satz des Pythagoras im rechtwinkligen Dreieck sagt aus, dass das Quadrat der Hypotenuse (der Strecke vom Ursprung zum Punkt auf dem Kreis, die immer 1 ist) gleich der Summe der Quadrate der beiden Katheten (die x- und y-Koordinaten des Punktes) ist.
Da der Radius des Einheitskreises immer 1 ist, ergibt sich die Identität:
x² + y² = 1
Wenn wir x = cos(α) und y = sin(α) setzen, erhalten wir die trigonometrische Identität:
(sin(α))² + (cos(α))² = 1
Diese Identität ist eine direkte Folge des Satzes des Pythagoras und gilt für jeden Winkel α. Sie beschreibt die Verbindung zwischen den beiden Hauptfunktionen der Trigonometrie, Sinus und Kosinus, und ist auf dem Einheitskreis leicht zu erkennen.
Beachte folgende Schreibweisen: (sin(α))² = sin²(α) ≠ sin(α)²
Seitenverhältnisse im rechtwinkligen Dreieck
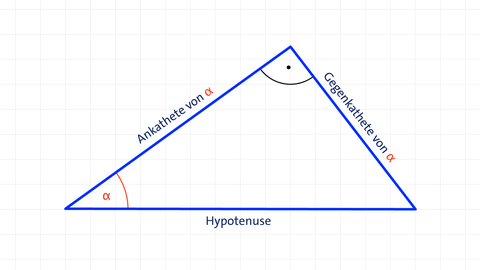
In einem rechtwinkligen Dreieck wird die dem rechten Winkel gegenüberliegende Seite als Hypotenuse und die zwei kleineren Seiten als Katheten bezeichnet. In diesem rechtwinkligen Dreieck wird die einem spitzen Winkel gegenüberliegende Kathete als Gegenkathete und die dem Winkel anliegende Kathete als Ankathete bezeichnet.
Die Winkel in rechtwinkligen Dreiecken legen die Seitenverhältnisse fest. So vereinbart man für diese Seitenverhältnisse feste Begriffe, und zwar Sinus (sin), Kosinus (cos), Tangens (tan) und Kotangens (cotan).
Beispielaufgabe: Seitenverhältnisse im rechtwinkligen Dreieck und Winkelfunktionswerte
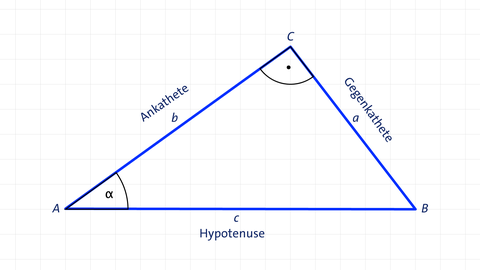
Berechne zum Winkel α den Sinus, den Kosinus, den Tangens und den Kotangens. Gib auch die Winkel im Dreieck an, wenn die Seite a = 3 Meter, die Seite b = 4 Meter und die Seite c = 5 Meter sind.
Beispielaufgabe: Winkelberechnung
Ein Maler streicht die Fassade eines Wohnhauses. Seine 5 Meter lange Leiter lehnt an der Hauswand. Der Abstand des Fußendes der Leiter von der Wand beträgt 1,5 Meter. Bestimme die Winkel α am Leiteranfang und den Winkel γ am Leiterende.
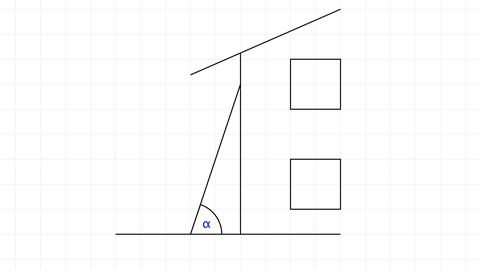
Beispielaufgabe: Steigung einer Geraden
Beispielaufgabe: Steigung einer Straße
Als Beifahrer bist du im Auto auf einer Landstraße unterwegs. Du siehst folgenden Warnhinweis:

Du fragst die Mitfahrer auf der Rückbank: "Wenn hier eine Steigung von 14% kommt, welchem Winkel gegenüber der Horizontalen entspricht diese Steigung?"