Hier lernst du, wie man rechtwinklige Dreiecke konstruiert und welche Eigenschaften sie haben. Außerdem erhältst du Informationen zum Lehrsatz des Pythagoras und zu weiteren Lehrsätzen in rechtwinkligen Dreiecken.
Ein rechtwinkliges Dreieck ist ein Dreieck, bei dem einer der Innenwinkel genau 90° beträgt, also ein rechter Winkel vorliegt.
Satz des Thales
Der Satz des Thales ist ein grundlegendes Ergebnis der Geometrie, das die Beziehung zwischen einem Kreis und einem rechtwinkligen Dreieck beschreibt.
Wichtige Eigenschaften eines rechtwinkligen Dreiecks:
- Rechter Winkel: Einer der drei Winkel beträgt immer 90°. Die beiden anderen Winkel sind jeweils kleiner als 90° und ergänzen sich zu 90° (da die Summe der Innenwinkel eines Dreiecks stets 180° beträgt).
- Hypotenuse: Die Seite gegenüber dem rechten Winkel wird als Hypotenuse bezeichnet und ist die längste Seite des rechtwinkligen Dreiecks.
- Katheten: Die beiden anderen Seiten, die den rechten Winkel einschließen, werden als Katheten bezeichnet. Sie sind kürzer als die Hypotenuse.
Satz des Pythagoras
Weitere Sätze im rechtwinkligen Dreieck
Beispielaufgabe: Berechnung der Kegelhöhe
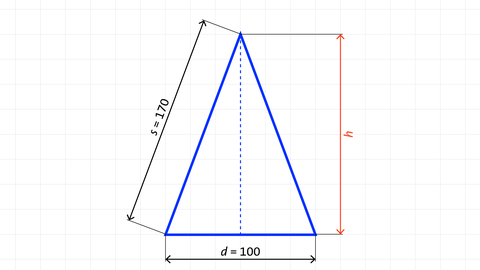
Ein Kegel hat den Durchmesser d = 100 mm und die Mantellänge s = 170 mm. Bestimme seine Kegelhöhe h.
Beispielaufgabe: Länge eines Fensterrahmenprofils
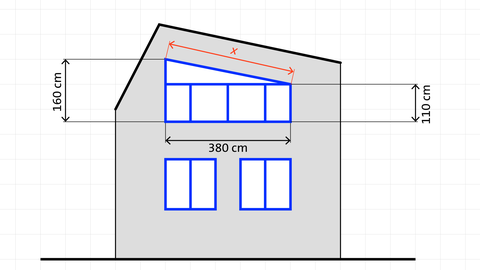
Das Spezialfenster eines Bürogebäudes muss ausgetauscht werden. Bestimme, auf welche Länge x (siehe Bild) das Fensterrahmenprofil (bzw. die Oberseite des Fensters) zugeschnitten werden muss.
Beispielaufgabe: Längenberechnung
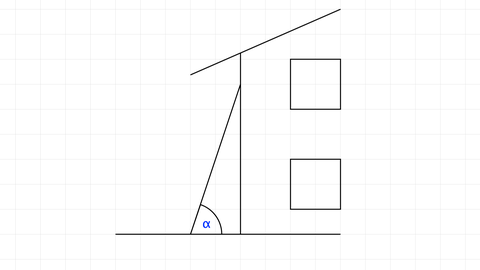
Ein Dachdecker möchte eine Regenrinne kontrollieren. Er lehnt seine 4 Meter lange Leiter an die Hauswand. Der Abstand des Fußendes der Leiter von der Wand beträgt 1,2 Meter. Bestimme, in welcher Höhe die Leiter die Hauswand berührt.