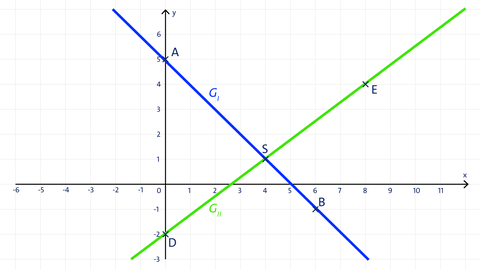
Aufgabe 1 Im rechtwinkligen Koordinatensystem sind die Graphen der linearen Gleichungssysteme x + 4y = 20 x + 4y = -8
BR; www.geogebra.org
Lösung zu a)
Zur Lösung der Aufgabe werden Punktkoordinaten in die Gleichung eingesetzt.
A(0|5) in (I): 4 ∙ 0 + 4 ∙ 5 = 20; 0 + 20 = 20;
B(6|-1) in (I): 4 ∙ 6 + 4 ∙ (-1) = 20; 24 - 4 = 20;
⇒ Die Gerade durch die Punkte A und B entspricht dem linearen Gleichungssystem (I).
Also müsste die Gerade durch die Punkte D und E zu (II) gehören.
D(0|-2) in (II): -3 ∙ 0 + 4∙(-2) = -8; 0 - 8 = -8;
E(8|4) in (II): -3 ∙ 8 + 4 ∙ 4 = -8; -24 + 16 = - 8;
⇒ Die Gerade durch die Punkte D und E entspricht dem linearen Gleichungssystem (II).
Lösung zu b)
Für die Koordinaten des Schnittpunkts S gilt: S(4|1)
S(4|1) in (I): 4 ∙ 4 + 4 ∙ 1 = 20; 16 + 4 = 20;
S(4|1) in (II): -3 ∙ 4 + 4 ∙ 1 = -8; -12 + 4 = - 8;
Der Punkt S(4|1) ist Element beider Gleichungen und somit Schnittpunkt der beiden Geraden.
Lösung zu c)
Für die Lösung des linearen Gleichungssystems bietet sich entweder das Einsetzverfahren oder das Additionsverfahren an, wegen des Terms 4y in beiden Linearen Gleichungen.
Gewählt wird das Additionsverfahren:
(I) 4x + 4y = 20 | ∙ (-1) x + 4y = -8
(I)' -4x - 4y = -20 x + 4y =-8
(I)' + (II) ∶ -7x = -28 ⇔ x = 4 x = 4 in (I) 4 ∙ 4 + 4 ∙ y = 20; y = 20; 4y = 4 ⇔ y = 1
Lösungsmenge: L = {(4|1)}
Aufgabe 2 Das folgende lineare Gleichungssystem istx + y = -3x + 2y = 8
Lösung zu a)
Einsetzverfahren :
(I) -2x + y = -3 | auflösen nach y y = 2x - 3 | einsetzen in (II)
(II) 3x + 2y = 8 x + 2 ∙ (2x - 3) = 8 | Terme zusammenfassen x + 4x - 6 = 8 ⇒ 7x = 14 ⇔ x = 2
x = 2 in (I)': y = 2x - 3; y = 2 ∙ 2 - 3 L = {(2|1)}
Lösung zu b)
Gleichsetzverfahren :
(I) -2x + y = -3 | mit 2 multiplizieren x + 2y = -6
(II) 3x + 2y = 8 | auflösen nach 2y : y = -3x + 8
(I)' -4x + 2y = -6 | auflösen nach 2y : y = 4x -6
(I)'' = (II)' 4x - 6 = -3x + 8 | Terme zusammenfassen x = 14 ⇔ x = 2 x = 2 in y = 2x - 3; y 1 ⇒ L = {(2|1)}
Lösung zu c)
Additionsverfahren :
(I) -2x + y = -3 | mit -2 multiplizieren: x - 2y = 6
(II) 3x + 2y = 8 x - 2y =6
(I)'+ (II) ⇒ 7x = 14 ⇔ x = 2
x = 2 in -2x + y = -3; -2 ∙ 2 + y = -3 y = -3 ⇔ y = 1 ⇒ L = {(2|1)}
Aufgabe 3 Das folgende lineare Gleichungssystem istx - 4y = -3x - 10y = 1
Lösung zu a)
Einsetzverfahren :
(I) x - 4y = -3 | auflösen nach x x = 4y - 3 | einsetzen in (II) x - 10y = 1
(II)' 3 ∙ (4y - 3) - 10y = 1 | Terme zusammenfassen y - 9 - 10y = 1 ⇒ 2y =10 ⇔ y = 5 y = 5 in x = 4y - 3; x = 4 ∙ 5 - 3 = 17 L = {(17|5)}
Lösung zu b)
Gleichsetzverfahren :
Beim Gleichsetzverfahren werden beide Gleichungen nach der gleichen Variablen aufgelöst und dann gleichgesetzt.
(I) x - 4y = -3 | mit 3 multiplizieren und nach 3x auflösen x = 12y - 9
(II) 3x - 10y = 1 | nach 3x auflösen x = 10y + 1
(I)' = (II)' 12y - 9 = 10y + 1 | Terme zusammenfassen y = 10 ⇔ y = 5
y = 5 in x - 4y = -3; x - 4 ∙ 5 = -3 x = 20 - 3 ⇔ x = 17 ⇒ L = {(17|5)}
Lösung zu c)
Additionsverfahren :
Beim Additionsverfahren werden die beiden Gleichungen so umgeformt, dass beim Addieren der Gleichungen eine Variable wegfällt.
(I) x - 4y = -3 | mit -3 multiplizieren x + 12y = 9
(II) 3x - 10y = 1 x + 12y = 9
(I)'+ (II) ⇒ 2y = 10 ⇔ y = 5
y = 5 in x - 4y = -3; x - 4 ∙ 5 = -3 ⇔ x = 20 - 3 x = 17 ⇒ L = {(17|5)}
Aufgabe 4 Das folgende lineare Gleichungssystem ist x + 3y = 3x = 3y + 15
Lösung zu a)
Einsetzverfahren :
(I) 2x + 3y = 3 | auflösen nach 3y y = -2x + 3 | einsetzen in (II)
(II) 4x = 3y +15 x = -2x + 3 + 15 | Terme zusammenfassen x =18 ⇔ x = 3
x = 3 in (I)' 3y = -2x + 3; 3y = -2 ∙ 3 + 3 = -6 + 3 y = -1 ⇒ L = {(3|-1)}
Lösung zu b)
Gleichsetzverfahren :
(I) 2x + 3y = 3 | mit 2 multiplizieren und nach 4x auflösen x = -6y + 6
(II) 4x = 3y + 15 x = -6y + 6
(I)' = (II) -6y + 6 = 3y + 15 | Terme zusammenfassen y = 9 ⇔ y = -1
y = -1 in 4x = 3y + 15; 4x = 3 ∙ (-1) + 15 = 12 ⇔ x = 3 L = {(3|-1)}
Lösung zu c)
Additionsverfahren :
(I) 2x + 3y = 3 x = 3y + 15 | -3y x - 3y = 15
(I) + (II)' 6x = 18 ⇔ x = 3
x = 3 in (I) : 2 ∙ 3 + 3y = 3 ⇔ 3y = 3 - 6y = -1 ⇒ L = {(3|-1)}
Aufgabe 5 Eine Mutter und ihre Tochter sind zusammen 60 Jahre alt. Die Mutter ist 24 Jahre älter als ihre Tochter.
Lösung zu a)
Zur Lösung der Aufgabe werden die Variablen x und y eingeführt. x und das Alter der Tochter mit y so gilt für den Satz „Eine Mutter und ihre Tochter sind zusammen 60 Jahre alt“ die lineare Gleichung x + y = 60. x = y + 24.
Zur Lösung der Aufgabe kann folgendes lineare Gleichungssystem verwendet werden: x + y = 60 x - y = 24
Es bietet sich hier das Additionsverfahren an, da bei der Addition der Gleichungen die Variable y eliminiert wird.
(I) + (II): 2x = 84 ⇔ x = 42 x = 42 in (I): 42 + y = 60 y = 60 - 42 ⇔ y = 18
Die Mutter ist also 42 Jahre und ihre Tochter 18 Jahre alt ⇒ L = {(42|18)}
Lösung zu b)
Mit je zwei Punkten können die Graphen der linearen Gleichungen gezeichnet werden.
(I) x + y = 60; x = 0: 0 + y = 60; y = 60 ⇒ A(0|60) x = 20: 20 + y = 60; y = 40 ⇒ B(20|40)
(II) x - y = 24 x = 0: 0 - y = 24; y = -24 ⇒ C(0|-24) x = 24: 24 - y = 24; y = 0 ⇒ D(24|0)
BR; www.geogebra.org