In dieser Folge lernst du, was eine lineare Gleichung ist und was ein lineares Gleichungssystem. Außerdem erfährst du, wie du ein lineares Gleichungssystem lösen kannst.
Lineare Gleichung mit zwei Variablen
Eine Gleichung der Form ax + by = c heißt lineare Gleichung mit zwei Variablen, dabei sind x und y Variablen, a und b Koeffizienten und c eine Konstante.
Beispielaufgabe: Lineare Gleichung
Gegeben ist die lineare Gleichung 2x - y = 3.
a) Gib die Koeffizienten der Gleichung an.
b) Bestimme zwei Lösungen der Gleichung.
c) Beschreibe, wie die zur Gleichung gehörende Gerade gezeichnet werden kann und zeichne die Gerade.
Lineares Gleichungssystem mit zwei Gleichungen
Zwei lineare Gleichungen mit zwei gemeinsamen Variablen („Unbekannten“) x und y nennt man ein lineares Gleichungssystem (LGS).
Anzahl der Lösungen eines linearen Gleichungssystems aus zwei Gleichungen mit zwei Unbekannten
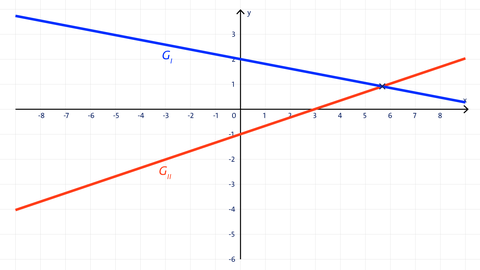
Eine eindeutige Lösung:
Die Geraden schneiden sich in einem Punkt.
Das Gleichungssystem hat genau eine Lösung.
Lösungsmenge: L = {(x|y)}
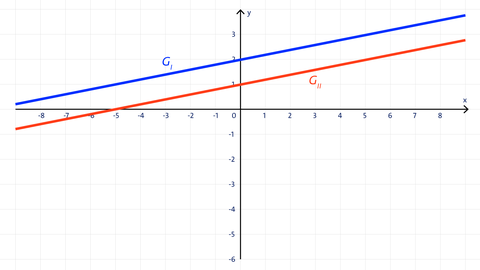
Keine Lösung:
Die Geraden sind parallel, aber nicht identisch. Die Geraden schneiden sich nie.
Das Gleichungssystem hat keine Lösung.
Lösungsmenge: L = { }
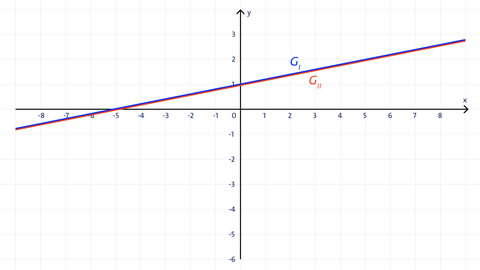
Unendlich viele Lösungen:
Die Geraden liegen aufeinander (identische Gleichungen).
Das Gleichungssystem hat unendlich viele Lösungen.
Lösungsmenge: L = {(x|y)|y = mx + t}
Lösungsmethoden linearer Gleichungssysteme
1. Grafische Lösung (die Geraden zeichnen und die Lösungsmenge ablesen)
Vorgehensweise bei der grafischen Lösung eines Linearen Gleichungssystems mit zwei Gleichungen:
a) Die zwei Gleichungen in die „Geradengleichung“ y = mx + t umformen.
b) Jeweils zwei Punkte der Geraden bestimmen.
c) Geraden durch die Punkte zeichnen und die Lösungsmenge L ablesen und angeben.
d) Probe durchführen.
Beispielaufgabe: Grafische Lösung
Löse das lineare Gleichungssystem grafisch.
2. Einsetzungsverfahren (eine Gleichung nach einer Variablen auflösen und in die andere einsetzen)
Vorgehensweise bei der Lösung eines Linearen Gleichungssystems mit zwei Gleichungen mit dem Einsetzverfahren:
a) Umformen: Man löst eine der zwei Gleichungen nach einer Variablen (z.B. y; abhängig von der Gleichung) auf.
b) Einsetzen: Der ermittelte Term für y wird in die andere Gleichung eingesetzt und die so entstandene Gleichung nach x aufgelöst.
c) Ermittelte Variable einsetzen: Die ermittelte Variable x wird in die nach y aufgelöste Gleichung ein und berechnet den Wert für y.
d) Lösungsmenge angeben.
Beispielaufgabe: Einsetzverfahren
Löse das lineare Gleichungssystem mit dem Einsetzverfahren.
3. Additionsverfahren (die Gleichungen so umformen, dass eine Variable durch Addition oder Subtraktion eliminiert wird)
Vorgehensweise bei der Lösung eines Linearen Gleichungssystems mit zwei Variablen mit dem Additionsverfahren:
a) Umformen: Man multipliziert eine Gleichung oder beide Gleichungen jeweils mit einer geeigneten Zahl, so dass durch die Addition der Gleichungen eine Variable eliminiert wird.
b) Gleichungen addieren: Die beiden bearbeiteten Gleichungen werden addiert (oder subtrahiert), so dass eine Variable „wegfällt“ und die Gleichung nach der verbliebenen Variable aufgelöst.
c) Variable einsetzen: Die ermittelte Variable in eine der beiden ursprünglichen Gleichungen einsetzen und den Wert der anderen Variablen bestimmen.
d) Lösungsmenge angeben.
Beispielaufgabe: Additionsverfahren
Löse das lineare Gleichungssystem mit dem Additionsverfahren.
4. Gleichsetzungsverfahren (beide Gleichungen nach der gleichen Variablen auflösen und gleichsetzen)
Vorgehensweise bei der Lösung eines Linearen Gleichungssystems mit zwei Variablen mit dem Gleichsetzungsverfahren (auch: Gleichsetzverfahren):
a) Umformen: Man formt beide Gleichungen nach der y-Variablen um.
b) Gleichungen gleichsetzen und nach x auflösen: Die beiden Gleichungen werden gleichgesetzt und nach x aufgelöst.
c) Fehlenden y-Wert berechnen und Lösungsmenge angeben: Der ermittelte x-Wert wird in eine der Ausgangsgleichungen eingesetzt und der y-Wert berechnet. Die Lösungsmenge ist dann der Schnittpunkt beider Graphen.
Das Gleichsetzungsverfahren findet vor allem Anwendung bei der Berechnung von Schnittpunkten zweier Graphen von Funktionen höherer Ordnung.
Beispielaufgabe: Gleichsetzungsverfahren
Löse das lineare Gleichungssystem mit dem Gleichsetzungsverfahren.
5. Lineare Gleichungssysteme bei anwendungsbezogenen Aufgaben
Strategie bei der Erstellung und Lösung anwendungsbezogener Aufgaben:
- Welche Größen sind in der Aufgabenstellung vorgegeben? Man überlegt zunächst, was durch die Variablen beschrieben werden soll. Dabei ist es hilfreich, die gesuchten Größen durch Unterstreichen oder mit einem Textmarker hervorzuheben.
- Welche Größen sind gesucht? Die gesuchten Größen werden mit den Variablen x und y bezeichnet.
- Wie stehen die mit Variablen bezeichneten Größen miteinander in Beziehung? Müssen die Variablen mit einer Ziffer oder Zahl multipliziert werden?
- Die mathematische Beziehung als Gleichung formulieren. Summen bzw. Differenzen der Variablen bilden. Für zwei Variablen sind zwei Gleichungen erforderlich.
- Welche Zahlenmenge muss dem Sachverhalt zugrunde gelegt werden? Dürfen z.B. nur ganze Zahlen vorkommen? Sind negative Werte erlaubt?
- Für die Lösung des Gleichungssystems ein geeignetes Lösungsverfahren wählen.
- Je nach Sachlage eines der beschriebenen Verfahren wählen.
- Die gefundene Lösung mittels Probe überprüfen. Die ermittelte Lösung muss auf Richtigkeit durch Einsetzen in die zwei Gleichungen überprüft werden.
Beispielaufgabe: Anwendungsbezogene Aufgabe
Luka startet mit seinem E-Bike auf einen Ausflug und radelt mit einer Durchschnittsgeschwindigkeit von 20 km/h los. Seine Mutter bemerkt, dass er Geldbörse und Handy vergessen hat, und fährt ihm mit dem Auto mit 60 km/h hinterher.
a) Wähle ein geeignetes Koordinatensystem und zeichne beide Graphen ein.
b) Ermittle den Zeitpunkt, wann die Mutter Luka einholt.
c) Bestätige durch Berechnung den ermittelten Treffpunkt T.