Übungen zu "Sekante" Aufgabe 1
Untersuche die Parabel mit der Funktionsgleichung f ( x ) = 1 2 x 2 + 2 x − 2 und die Gerade mit der Funktionsgleichung g ( x ) = − x + 6 auf gemeinsame Punkte.
Lösung
Schritt 1: Funktionsterme gleichsetzen: f (x ) = g (x )
1 2 x 2 + 2 x − 2 = − x + 6
Schritt 2: Gleichung durch Äquivalenzumformung so umformen, dass eine quadratische Gleichung der Form ax ² + bx + c = 0 vorliegt.
1 2 x 2 + 2 x − 2 = − x + 6 | + x − 6
Schritt 3: Mittels Diskriminante D = b ² - 4ac ermitteln, ob gemeinsame Schnittpunkte zwischen der Gerade und der Parabel existieren.
D = b 2 − 4 ac = 3 2 − 4 · 1 2 · ( − 8 ) = 9 + 16 = 25
D = 25 > 0 ⟹ es existieren zwei Schnittpunkte
Schritt 4: Schnittpunkte existieren, deshalb die x -Koordinaten mithilfe der Lösungsformel bestimmen, die y -Koordinaten berechnen und die Punkte angeben.
Die Koeffizienten a = 1 2 und b = 3 der quadratischen Gleichung in die Lösungsformel einsetzen, die Diskriminante D = 25 kann übernommen werden.
x 1 ; 2 = − b ± b 2 − 4 ac 2 a = − 3 ± 25 2 · 1 2 = − 3 ± 5 1 ; x 1 = − 3 + 5 1 = 2 ; x 2 = − 3 − 5 1 = − 8
Zur Ermittlung der y -Koordinate des Schnittpunkts werden die x -Werte in die Geradengleichung eingesetzt (einfachere Lösungsmöglichkeit).
y₁ = g (x ₁) = -2 + 6 = 4 ⟹ S₁ (2|4); y ₂ = g (x ₂) = -(-8) + 6 = 14 ⟹ S₂(-8|14)S ₁ (2|4) und S₂(-8|14) sind die gesuchten Schnittpunkte.
Aufgabe 2 Untersuche die Parabel mit der Funktionsgleichung f (x ) = -x ² + 3x + 4 und die Gerade mit der Funktionsgleichung g (x ) = 4 auf gemeinsame Punkte.
Lösung
Schritt 1: Funktionsterme gleichsetzen: f (x ) = g (x )
-x ² + 3x + 4 = 4
Schritt 2: Gleichung durch Äquivalenzumformung so umformen, dass eine quadratische Gleichung der Form ax ² + bx + c = 0 vorliegt.
-x ² + 3x + 4 = 4 | - 4x ² + 3x = 0
Schritt 3: Mittels Diskriminante D = b ² - 4ac ermitteln, ob gemeinsame Schnittpunkte zwischen der Gerade und der Parabel existieren.
D = b ² - 4ac = 3² - 4 ∙ (-1) ∙ 0 = 9 - 0 = 9
Schritt 4: Schnittpunkte existieren, deshalb die x -Koordinaten mithilfe der Lösungsformel bestimmen, die y -Koordinaten berechnen und die Punkte angeben.
Die Koeffizienten a = -1, b = 3 und c = 0 der quadratischen Gleichung in die Lösungsformel einsetzen.
x 1 ; 2 = − b ± b 2 − 4 ac 2 a = − 3 ± 3 2 − 4 · ( − 1 ) · 0 2 · ( − 1 ) = − 3 ± 3 − 2 ; x 1 = − 3 + 3 − 2 = 0 ; x 2 = − 3 − 3 − 2 = 3
y ₁ = g (x ₁) = 4 ⟹ S₁(0|4); y ₂ = g (x ₂) = 4 ⟹ S₂(3|4)S₁(0|4) und S₂(3|4) sind die gesuchten Schnittpunkte.
Aufgabe 3 Bestimme die Lage der Parabel mit der Gleichung f (x ) = x ² - 4x + 5 und der Geraden mit der Gleichung g (x ) = x + 1 zueinander. Nutze die Diskriminante.
Lösung
Schritt 1: Funktionsterme gleichsetzen: f (x ) = g (x )
x ² - 4x + 5 = x + 1
Schritt 2: Gleichung durch Äquivalenzumformung so umformen, dass eine quadratische Gleichung der Form ax ² + bx + c = 0 vorliegt.
x ² - 4x + 5 = x + 1 | - x -1x ² - 5x + 4 = 0
Schritt 3: Mittels Diskriminante D = b ² - 4ac ermitteln, ob gemeinsame Schnittpunkte zwischen der Gerade und der Parabel existieren.
D = b ² - 4ac = (-5)² - 4 ∙ 1 ∙ 4 = 25 - 16 = 9
Aufgabe 4 Maximal wie viele Schnittpunkte hat eine Parabel mit einer Gerade?
Lösung
Falls D > 0 können maximal zwei Schnittpunkte vorliegen.
Aufgabe 5 Was sagt die Diskriminante D = b ² - 4ac aus, wenn du f (x ) = g (x ) gleichsetzt?
Lösung
Die Diskriminante zeigt an, wie viele Schnittpunkte eine Parabel und eine Gerade haben.
Aufgabe 6 Wie nennt man eine Gerade, die zwei Schnittpunkte mit einer Parabel hat?
Lösung
Diese Gerade wird Sekante genannt.
Übungen zu "Tangente" Aufgabe 7
Untersuche die Parabel mit der Funktionsgleichung f ( x ) = − 1 2 x 2 − 2 x + 6 und die Gerade mit der Funktionsgleichung g ( x ) = − 2 x + 6 auf gemeinsame Punkte.
Lösung
Schritt 1: Funktionsterme gleichsetzen: f (x ) = g (x )
− 1 2 x 2 − 2 x + 6 = − 2 x + 6
Schritt 2: Gleichung durch Äquivalenzumformung so umformen, dass eine quadratische Gleichung der Form ax ² + bx + c = 0 vorliegt.
− 1 2 x 2 − 2 x + 6 = − 2 x + 6 | + 2 x − 6
Schritt 3: Mittels Diskriminante D = b ² - 4ac ermitteln, ob gemeinsame Schnittpunkte zwischen der Gerade und der Parabel existieren.
D = b ² - 4ac = 0² - 4 ∙ 0 ∙ 0 = 0 - 0 = 0
Schritt 4: Berührpunkt existiert, deshalb die x -Koordinate mithilfe der Lösungsformel bestimmen, die y -Koordinate berechnen und den Punkt angeben.
Die Koeffizienten a = − 1 2 und b = 0 der quadratischen Gleichung in die Lösungsformel einsetzen, die Diskriminante D = 0 kann übernommen werden.
x 1 ; 2 = − b ± b 2 − 4 ac 2 a = − 0 ± 0 2 · ( − 1 2 ) = − 0 ± 0 − 1 ; x 1 = x 2 = − 0 − 1 = 0
Zur Ermittlung der y - Koordinate des Berührpunkts werden die x -Werte in die Geradengleichung eingesetzt (einfachere Lösungsmöglichkeit). y = g (x ) = -2 ∙ 0 + 6 = 0 + 6 = 6 ⟹ B(0|6)B(0|6 ).
Aufgabe 8 Was bedeutet es, wenn eine Gerade eine Parabel berührt?
Lösung
b) Es gibt genau einen gemeinsamen Punkt.
Aufgabe 9 Benenne die Gerade, die die Parabel berührt:
Lösung
b) Die Gerade heißt Tangente.
Aufgabe 10 Welche Aussage trifft zu, wenn D = 0 bei der Gleichung f (x ) = g (x )?
Lösung
c) Die Gerade berührt die Parabel.
Übungen zu "Passante" Aufgabe 11
Untersuche die Parabel mit der Funktionsgleichung f ( x ) = − 1 2 x 2 + 3 2 x + 2 und die Gerade mit der Funktionsgleichung g ( x ) = − 1 2 x + 5 auf gemeinsame Punkte.
Lösung
Schritt 1: Funktionsterme gleichsetzen: f (x ) = g (x )
− 1 2 x 2 + 3 2 x + 2 = − 1 2 x + 5
Schritt 2: Gleichung durch Äquivalenzumformung so umformen, dass eine quadratische Gleichung der Form ax ² + bx + c = 0 vorliegt.
− 1 2 x 2 + 3 2 x + 2 = − 1 2 x + 5 | + 1 2 x − 5
Schritt 3: Mittels Diskriminante D = b ² - 4ac ermitteln, ob gemeinsame Schnittpunkte zwischen der Gerade und der Parabel existieren.
D = b 2 − 4 a c = 2 2 − 4 · ( − 1 2 ) · ( − 3 ) = 4 − 6 = − 2
D < 0 (negativ) ⟹ es existiert kein Schnittpunkt zwischen Parabel und Gerade.
Aufgabe 12
Zeige, dass die Gerade g ( x ) = 0 ( x -Achse ) eine Passante zur Parabel mit der Funktionsgleichung f ( x ) = 1 2 x 2 − x + 3 2 ist und ermittle den kürzesten vertikalen Abstand d von Parabel und Passante.
Lösung
Nach Aufgabenstellung ist der kürzeste Abstand von der Parabel zur x -Achse gesucht. Es ist als Erstes zu zeigen, dass die x -Achse eine Passante zur Parabel ist und somit keinen Schnittpunkt mit der x -Achse hat.f (x ) = g (x )
Diskriminante D = b ² - 4ac untersuchen.
D = ( − 1 ) 2 − 4 · ( 1 2 ) · ( 3 2 ) = 1 − 3 = − 2
D < 0 (negativ) ⟹ es existiert kein Schnittpunkt zwischen Parabel und der x -Achse, also ist die x -Achse Passante zur Parabel.
Kürzesten Abstand ermitteln:
Die Funktionsgleichung f ( x ) = 1 2 x 2 − x + 3 2 ist eine nach oben geöffnete Parabel, deren tiefste Stelle der Scheitelpunkt der Parabel ist.
Der kürzeste Abstand der Parabel von der x -Achse ist somit die y -Koordinate des Scheitelpunkts.
Scheitelpunkt der Parabel ermitteln:
Für die x -Koordinate des Scheitelpunkts gilt: x s = − b 2 a = − ( − 1 ) 2 · 1 2 = 1 1 = 1
Für die y -Koordinate des Scheitelpunkts gilt: y s = f ( x s ) = f ( 1 ) = 1 2 ( 1 ) 2 − 1 + 3 2 = 1
Der tiefste Punkt der Parabel ist der Scheitelpunkt S(1|1), also liegt die y -Koordinate 1 LE über der x -Achse, somit ist der kürzeste Abstand von Parabel und Passante 1 LE .
Aufgabe 13 Erläutere, was der Begriff Passante im Zusammenhang mit einer Parabel und einer Geraden bedeutet.
Lösung
Die Gerade hat keinen Schnittpunkt mit der Parabel.Geraden mit einer Parabel bedeutet das: f (x ) = g (x ) hat keine Lösung .Diskriminante D < 0
Aufgabe 14 Zeige, wie man ohne die Graphen einer quadratischen und einer linearen Funktion bestimmen kann, dass eine Passante vorliegt.
Lösung
Die beiden Funktionsterme gleichsetzen und durch Äquivalenzumformung so umformen, dass eine quadratische Gleichung der Form ax ² + bx + c = 0 vorliegt.b ² - 4ac ermitteln, ob gemeinsame Schnittpunkte zwischen Geraden und Parabel existieren. Ist die Diskriminante D < 0 (negativ), dann handelt es sich bei der Geraden um eine Passante.
Aufgabe 15 Gib an, was für eine Gerade und eine Parabel gilt, wenn nach Gleichsetzen der Funktionsterme und nach Äquivalenzumformung die Diskriminante D < 0 ist.
Lösung
c) Parabel und Gerade haben weder Schnittpunkte noch einen Berührpunkt.
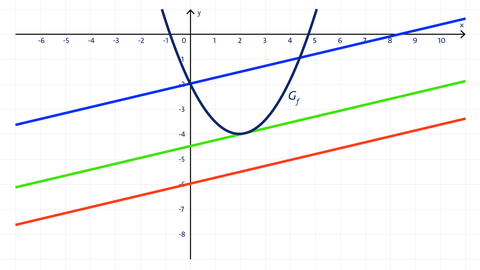
Aufgabe 16 Benenne die Bezeichnung der Geraden
BR; www.geogebra.org
Lösung
a) Gerade in blauer Farbe: Sekante