Stauchen und Strecken einer Parabel

In dieser Folge lernst du, welche Auswirkung der Wert a auf die Form der Parabel hat und wie man quadratische Funktionsgleichungen in verschiedenen Formen darstellen kann.

Stauchen und Strecken einer Parabel

Der Wert a in einer quadratischen Gleichung ist der Zahlenfaktor im quadratischen Glied und bestimmt, ob die Parabel:

gestaucht (flach) oder gestreckt (steil) ist.
nach oben oder nach unten geöffnet ist.

Der Wert a

$Die Graphen der Funktionen f (x) = a x^{2} mit a \neq 0 und x \in ℝ sind Parabeln, die jedoch für a \neq 1 bzw. a \neq - 1 eine andere Form als die Normalparabel aufweisen.$

Einfluss des Wertes a auf die Form der Parabel

Ändere die Werte von a und beobachte die Auswirkung auf die Parabel:

Beginne mit a = 1 und bewege den Schieberegler langsam nach rechts bis a = 5 und notiere deine Beobachtung.
Bewege den Schieberegler nun wieder nach links in den negativen Bereich bis a = -5 und notiere deine Beobachtung.

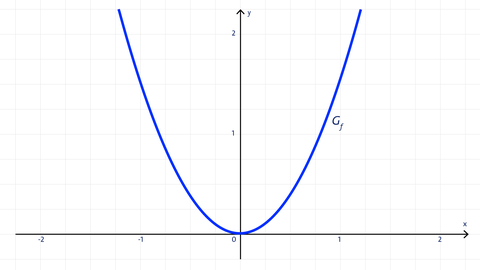
Die Parabel der Form f(x) = y = ax² mit a ≠ 0 ist nach oben geöffnet, falls a > 0.

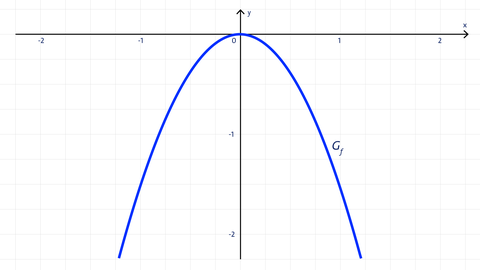
Die Parabel der Form f(x) = y = ax² mit a ≠ 0 ist nach unten geöffnet, falls a < 0.

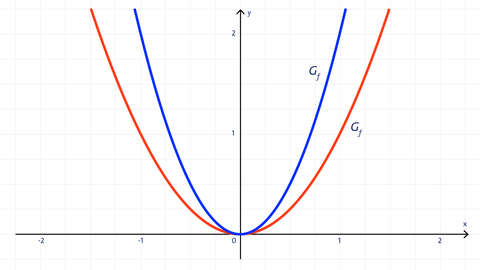
Die Parabel der Form f(x) = y = ax² mit a ≠ 0 ist enger als die Normalparabel, falls |a| > 1.

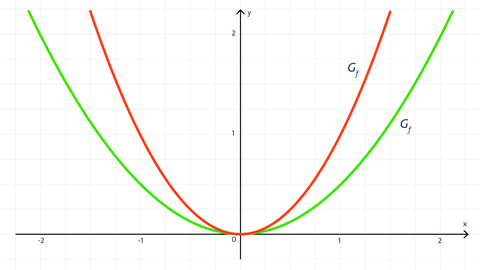
Die Parabel der Form f(x) = y = ax² mit a ≠ 0 ist weiter als die Normalparabel, falls |a| < 1.

Beispielaufgabe: Ermittlung des Wertes a

Verschiedene Parabeln im Koordinatensystem — BR

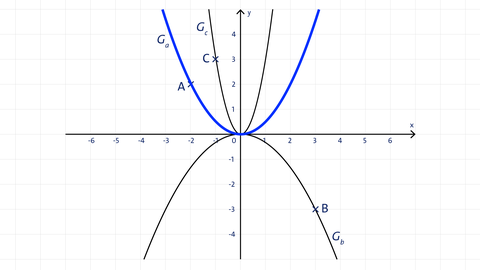
Die abgebildeten Parabeln im Koordinatensystem haben die Funktionsgleichungen y = ax².

Lies die Koordinaten der Punkte A, B, und C ab und bestimme die Funktionsgleichungen.

Darstellungsformen quadratischer Funktionen

Quadratische Funktionen können auf drei verschiedenen Formen dargestellt werden:

Scheitelpunktform (Scheitel der Parabel kann bestimmt werden)
Allgemeine Form (ausmultiplizierte Form – Ordinatenschnittpunkt kann bestimmt werden)
Faktorisierte Form (Nullstellenform – Nullstellen können bestimmt werden; diese Form kommt häufig bei Prüfungen vor)

Die Terme
(I) (x + 3)² - 4
(II) x² + 6x + 5 und
(III) (x + 5) ∙ (x + 1)
sind äquivalent. Sie können durch algebraische Umformungen ineinander umgeformt werden.

(I) (x + 3)² - 4 = x² + 6x + 9 - 4 = x² + 6x + 5 (II)

(III) (x + 5) ∙ (x + 1) = x² + x + 5x + 5 = x² + 6x + 5 (II)

Die Terme (I), (II) und (III) gehören demnach zur gleichen Funktion y = x² + 6x + 5.
Die verschiedenen Schreibweisen der Funktionsterme bieten den Vorteil, dass sie unterschiedliche Informationen vermitteln können.

Parabel zu Schreibweisen von Funktionstermen — BR

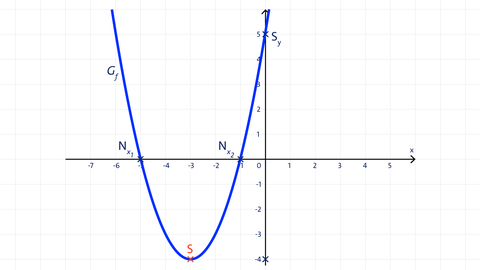
Aus der Scheitelpunktform f(x) = (x + 3)² - 4 kann der Scheitelpunkt S(-3|-4) abgelesen werden.

$Aus der allgemeinen Form f (x) = x^{2} + 6 x + 5 kann der Schnittpunkt des Graphen mit der y -Achse S_{y} (0 | 5) abgelesen werden, denn es gilt f (0) = 5 .$

Aus der Nullstellenformf(x) = (x + 5) ∙ (x + 1) können die Nullstellenx₁ und x₂ der quadratischen Funktion abgelesen werden, denn es gilt: f(-5) = 0 und f(-1) = 0 ⟹ x₁ = -5 und x₂ = -1 sind die Nullstellen von f.

Falls bei a ∙ x² der Faktor a ≠ 1 ist, so tritt der Faktor a auch in der Scheitelpunktform f(x) = a(x - xₛ)² + yₛ und der Nullstellenform f(x) = a(x - x₁) ∙ (x - x₂) auf.

Beispielaufgaben: Umformen von Funktionsgleichungen

Beispielaufgabe 1

$Ermittle für den Funktionsterm in der Scheitelpunktform f (x) = \frac{1}{2} {(x - 2)}^{2} - 2$

a) die allgemeine Form der quadratischen Gleichung.
b) die Nullstellenform der quadratischen Gleichung.

Beispielaufgabe 2

Ermittle für den Funktionsterm in der allgemeinen Form f(x) = -x² - 2x + 3

a) die Nullstellenform der quadratischen Gleichung.
b) die Scheitelpunktform der quadratischen Gleichung.

Beispielaufgabe 3

$Ermittle für den Funktionsterm in Nullstellenform f (x) = - \frac{3}{4} (x + 1) \cdot (x - 3)$

a) die allgemeine Form der quadratischen Gleichung.
b) die Scheitelpunktform der quadratischen Gleichung.

Stauchen und Strecken einer Parabel