In diesem Kapitel lernst du, was die einfachste quadratische Funktion ist, wie eine Normalparabel gezeichnet wird und wie die Normalparabel im Koordinatensystem verschoben werden kann.
Quadratische Funktionen
Eine quadratische Funktion ist eine Funktion, bei der die Variable x zum Quadrat im Funktionsterm vorkommt. Der Graph einer quadratischen Funktion heißt Parabel.
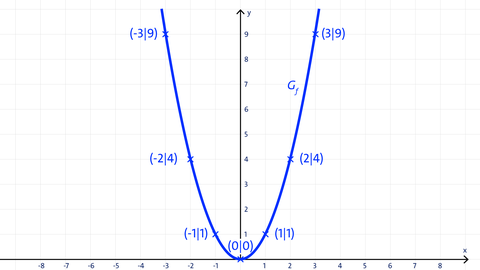
Beispielaufgabe: Wertetabelle und Graph der Funktion f mit f(x) = x²
Eine Wertetabelle ist eine Tabelle, in der aus der Definitionsmenge x-Werte gewählt werden und durch Einsetzen in die Funktionsgleichung die zugehörigen Funktionswerte y = f(x) berechnet werden.
f(-3) = (-3)² = 9
f(-2) = (-2)² = 4
f(-1) = (-1)² = 1
f(0) = (0)² = 0
f(3) = (3)² = 9
f(2) = (2)² = 4
f(1) = (1)² = 1
Diese Ergebnisse werden in die Wertetabelle eingetragen.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = f(x) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Die Wertepaare (x|y) werden in ein rechtwinkliges Koordinatensystem eingetragen, miteinander verbunden und ergeben dann den Graphen der Funktion.
Verschiebung der Normalparabel in x-Richtung
Wird die Normalparabel mit der Funktionsgleichung f(x) = x² und dem Scheitelpunkt S(0|0) auf der x-Achse verschoben, so verschiebt sich der Scheitel S auf der x-Achse.
Beispielaufgabe: Vergleich von Graphen
Vergleiche die Graphen der Funktionen:
f(x) = x²
f(x) = (x - 2)² und
f(x) = (x + 2)²
Einfluss des Wertes b auf die Verschiebung der Parabel auf der x-Achse
Ändere die Werte von b und beobachte die Auswirkung auf die Parabel.
Beginne mit b = 1.
Verändere dann b von -5 bis 5 und beobachte den Scheitel der Parabel.
Beispielaufgabe: Scheitelpunkt und Graph einer auf der x-Achse verschobenen Parabel
Bestimme aus dem Term der Funktion f mit f(x) = (x + 1)²
a) den Scheitelpunkt der Parabel und
Verschiebung der Normalparabel in y-Richtung
Betrachtet man die Geraden der linearen Funktionsgleichungen f(x) = m ∙ x und f(x) = m ∙ x + t, so gibt der Wert t die parallele Verschiebung der Geraden in y-Richtung an, wobei der Betrag von t das Ausmaß und das Vorzeichen von t die Richtung der Verschiebung angeben.
Diese Betrachtung gilt nicht nur für Graphen linearer Funktionen, sondern auch für Graphen quadratischer Funktionen.
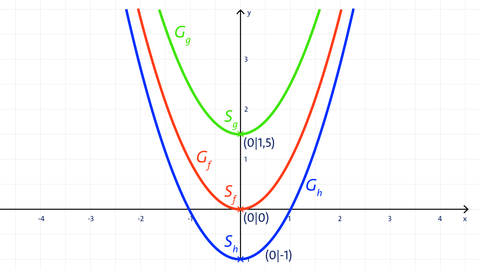
Wird zur Gleichung f(x) = x² eine Konstante c addiert, so ergibt sich die Funktionsgleichung f(x) = x² + c. Dadurch wird auch der Graph der Parabel in y-Richtung verschoben. Der Scheitelpunkt wird dann auch von S(0|0) zum Scheitelpunkt S(0|c) auf der y-Achse verschoben.
Beispielaufgabe: Verschiebung der Parabel auf der y-Achse
Vergleiche die Graphen der Funktionen:
f(x) = x² + 3
f(x) = x²
f(x) = x² - 2
Die Funktionswerte werden in einer Wertetabelle berechnet und dann die Graphen der Gleichungen skizziert.
Einfluss des Wertes c auf die Verschiebung der Parabel auf der y-Achse.
Ändere die Werte von c und beobachte die Auswirkung auf die Parabel.
Beginne mit c = 0.
Verändere dann c von -5 bis 5 und beobachte den Scheitel der Parabel.
Beispielaufgabe: Parabeln auf der y-Achse verschoben
Die Graphen der Parabeln g und h sind gegenüber der Normalparabel f mit f(x) = x² auf der y-Achse verschoben.
Verschiebung der Normalparabel in x- und y-Richtung
Ausgehend von einer Parabel f(x) = x² mit dem Scheitel S(0|0) im Ursprung hat der Scheitel bei einer Verschiebung mit der Größe c nur in y-Richtung die Koordinaten S(0|c) und die Funktionsgleichung lautet:
f(x) = x² + c
Verschiebt man die Parabel f(x) = x² mit dem Scheitel S(0|0) aus dem Ursprung um den Wert b nur in x-Richtung, hat ihr Scheitel die Koordinaten S(b|0) und die Funktionsgleichung dieser Parabel lautet:
f(x) = (x - b)²
Macht man nun eine Kombination dieser Verschiebungen mit der Parabel f(x) = x² aus dem Ursprung mit dem Scheitel S(0|0) in y-Richtung um den Wert c und in x-Richtung um den Wert b, so hat der Scheitel die Koordinaten S(b|c) und die Funktionsgleichung lautet:
f(x) = (x - b)² + c
Beispielaufgabe: Verschiebung der Normalparabel in x- und y-Richtung
Vergleiche die Graphen der Funktionen:
g: g(x) = (x + 2)² - 1
f: f(x) = x²
h: h(x) = (x - 2)² + 1
Einfluss des Wertes b und c auf die Verschiebung des Scheitelpunkts der Parabel
Ändere die Werte von b und c und beobachte die Auswirkung auf die Parabel.
Beginne mit b = c = 0.
Bewege die Schieberegler und vergleiche mit der Theorie.
Beispielaufgabe: Scheitelpunkt S aus Funktionsgleichung bestimmen
Bestimme den Scheitelpunkt S der Funktionen f: f(x) = (x - 3)² - 2 und g: g(x) = (x + 2)² + 3.