In dieser Folge lernst du, was eine lineare Funktion ist und wie deren Graphen aussehen. Außerdem erfährst du, was die Steigung und der y-Achsenabschnitt einer linearen Funktion bedeuten und wie du sie bestimmen kannst.
Eine lineare Funktion beschreibt einen proportionalen Zusammenhang zwischen zwei Größen.
Gerade durch zwei Punkte
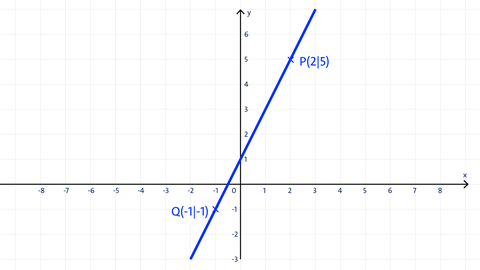
Die Punkte P(2|5) und Q(-1|-1) befinden sich im I. und III. Quadranten in einem rechtwinkeligen Koordinatensystem.
Zeichnet man eine Linie durch die Punkte P und Q, ergibt sich eine Gerade. Diese Gerade ist der Graph einer linearen Funktion mit der Funktionsgleichung f: f(x) = y = m∙x + t. Die Variable m ist die Steigung des Graphen und gibt das Verhältnis der Katheten in einem Steigungsdreieck wieder und es gilt:
Mit den Punkten P und Q kann somit die Funktionsgleichung der linearen Funktion f bestimmt werden.
P(2|5); Q(-1|-1)
Bestimmung der Steigung m:
⇒ f(x) = y = 2x + t
Zur Ermittlung der Variablen t werden die Punktkoordinaten von P oder Q in die Gleichung eingesetzt:
P(2|5): 5 = 2∙2 + t ⇔ t = 1
⇒ f: f(x) = y = 2x + 1
Lineare Funktion – Grundlagen
Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y einer Wertemenge W zu.
Hat der Graph der linearen Funktion mit der Funktionsgleichung y = m∙x + t die Steigung m = 0 (y = 0∙x + t ⇒ y = t), so ist der Graph eine Parallele zur x-Achse.
Eine solche Funktion nennt man konstante Funktion mit der Funktionsgleichung f(x) = y = t.
Der Graph einer linearen Funktion mit dem y-Achsenabschnitt t = 0 und beliebigem m ≠ 0 hat die Funktionsgleichung f(x) = y = m∙x und verläuft durch den Ursprung und wird deshalb als Ursprungsgerade bezeichnet.
Beispielaufgabe: Einfluss von Steigung m und y-Achsenabschnitt t
Ändere in der folgenden interaktiven Grafik die Werte von m und t und beobachte die Auswirkung auf die Gerade.
a) Beginne mit m = 1 und t = 0: f(x) =1∙x
Verändere dann nur die Steigung m.
b) Stelle wieder die Funktionsgleichung auf: f(x) =1∙x
Verändere jetzt nur den y-Achsenabschnitt t.
Steigung des Graphen einer linearen Funktion
Beispielaufgabe: Steigung
Du fährst auf der Autobahn mit konstanter Geschwindigkeit und legst in t = 3 min eine Strecke von
s = 5 km zurück.
a) Vervollständige die Wertetabelle:
| [t in min] x | 0 | 3 | 6 | 12 | 30 | 60 |
| [s in km] y | 0 | 5 |
b) Zeichne den Graphen der linearen Funktion in ein Koordinatensystem, bestimme die Steigung m und gib die Funktionsgleichung an.
Steigung m und Steigungsdreieck
Experimentiere mit dem folgenden interaktiven Applet und beobachte den Zusammenhang zwischen der Steigung m und dem dazugehörigen Steigungsdreieck. Beginne mit m = 1 und verändere dann die Steigung m .
Der y-Achsenabschnitt t des Graphen
Beispielaufgabe
Bei einer mehrtägigen Tour legt ein Fahrradfahrer am ersten Tag eine Strecke von s = 20 Kilometer zurück. Am nächsten Tag beginnt er erneut bei t = 0, ist aber am Vortag schon 20 km gefahren. Der Radfahrer fährt weiterhin mit der gleichen durchschnittlichen Geschwindigkeit wie am vorherigen Tag, nämlich 20 km/h. Das bedeutet, dass der Graph zum Zeitpunkt t = 0 nicht bei y = 0 startet, sondern bei y = 20, und anschließend linear ansteigt. Betrachtet man den Verlauf des Graphen in negativer x-Richtung, erkennt man, dass der Radfahrer am Vortag bereits 60 Minuten mit dem Fahrrad unterwegs war.
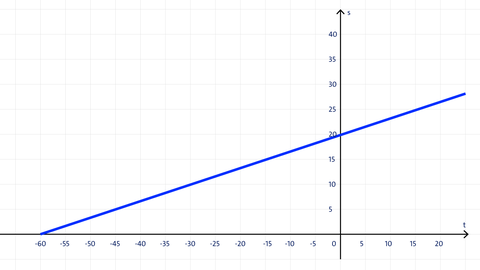
Die Funktionsgleichung dazu lautet:
Für die Definitionsmenge Dₕ gilt: Dₕ = [-60; ∞ [
Beispiel zur Bestimmung der Funktionsgleichung
f(x) = mx + t einer linearen Funktion
Vorgehensweise:
Bestimmung der Steigung m:
Bestimmung des y-Achsenabschnitts t: