In diesem Kapitel lernst du, was Variablen sind und wie sie zugeordnet werden, welche Bedeutung eine Wertetabelle hat und was eine Funktionsgleichung ist. Außerdem erfährst du, was der Graph einer Funktion ist.
Eine Funktion f ist eine Zuordnungsvorschrift x ↦ y = f(x), die jedem x-Wert aus der Definitionsmenge D genau einen y-Wert aus der Wertemenge W zuordnet.
Definitionsmenge D und Wertemenge W einer Funktion
Beispielaufgabe: Definitionsmenge D und Wertemenge W bei anwendungsbezogenen Aufgaben
Bei den linearen und quadratischen Funktionen ist die Definitionsmenge D = IR. Für die Wertemenge W bei linearen Funktionen gilt W = IR. Bei quadratischen Funktionen ist die Wertemenge W vom Funktionsterm abhängig. Ist jedoch eine Funktion gegeben, deren Variable die Zeit t ist, so ist die Definitionsmenge D eingeschränkt, denn der Zeitpunkt der Messung beginnt bei t = 0.
Gib die Definitionsmenge D und die Wertemenge W eines Sportlers beim 100-Meter-Sprint an.
Schreibweise für Funktionen
Funktionen werden mit Kleinbuchstaben f, g, h, usw. bezeichnet. Dargestellt werden kann die Funktion als Zuordnungsvorschrift f: x ↦ y (Sprechweise: „Funktion f, jedem x wird zugeordnet ein y“, oder „x wird abgebildet auf y“) oder als Funktionsgleichung f: y = f(x) (Sprechweise: „Funktion f, der Funktionswert an der Stelle x ist der y-Wert“). Die Variable x wird als unabhängige Variable bezeichnet (x kann frei aus der Definitionsmenge D gewählt werden), y wird als die von x abhängige Variable bezeichnet.
Die Wertetabelle zu einer Funktion
Eine Wertetabelle ist ein Hilfsmittel in der Mathematik, um eine Funktion systematisch zu untersuchen. Sie zeigt, welchen Funktionswert f(x) man für bestimmte x-Werte bekommt, also sozusagen „Eingabe → Ausgabe“.
Beispiel für eine Wertetabelle mit Beispielaufgabe
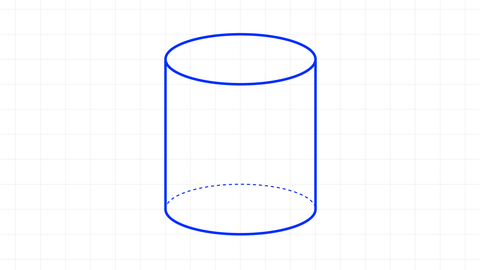
Ein zylindrisches Gefäß wird gleichmäßig mit Wasser gefüllt, das zufließt. Die Wassersäule im Gefäß steigt pro Minute um 0,5 cm.
a) Erstelle eine Wertetabelle, die den Sachverhalt in den ersten 8 Minuten beschreibt.
b) Gib die Funktionsgleichung an.
c) Zeichne den Graphen der Funktion.
Überprüfung, ob ein Graph ein Funktionsgraph ist
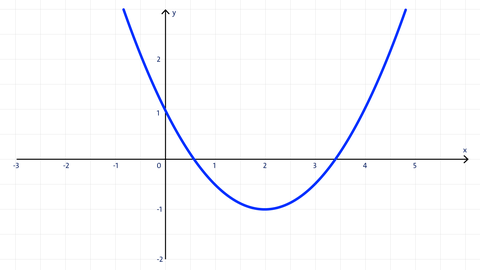
Eine Funktion ordnet jedem x-Wert aus der Definitionsmenge genau einen y-Wert aus der Wertenmenge zu. Wird der Graph der Funktion gezeichnet, so hat jede Parallele zur y-Achse genau einen Schnittpunkt mit dem Graphen. Gibt es für einen Graphen mehr als einen Schnittpunkt mit einer Parallelen zur y-Achse, so handelt es sich um den Graphen einer Relation.
Beispielaufgabe: Gehört der Graph zu einer Funktion?
Gib an, bei welchen Graphen es sich um einen Funktionsgraph handelt.
a)
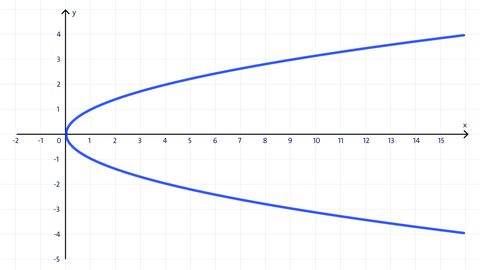
b)