In dieser Folge lernst du, wie die Achsen in einem kartesischen Koordinatensystem bezeichnet werden, wie Punkte in das Koordinatensystem eingetragen werden und wie man die vier Felder im Koordinatensystem bezeichnet.
Ausgehend von einem festen Bezugspunkt, dem Schnittpunkt der beiden Koordinatenachsen, lässt sich die Position eines Punktes eindeutig durch ein Zahlenpaar (x|y) bestimmen.
Aufbau, Merkmale und Definition des kartesischen Koordinatensystems
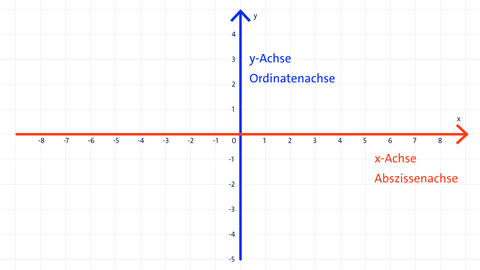
- Die Achsen sind Geraden. Die waagerechte Achse bezeichnet man als x-Achse oder Abszissenachse, die senkrechte Achse als y-Achse oder Ordinatenachse.
- Die Achsen stehen paarweise senkrecht (orthogonal) aufeinander.
- Der Schnittpunkt beider Achsen heißt Nullpunkt oder Ursprung O(0|0).
Zuordnung und Eintrag eines Punktes in das Koordinatensystem
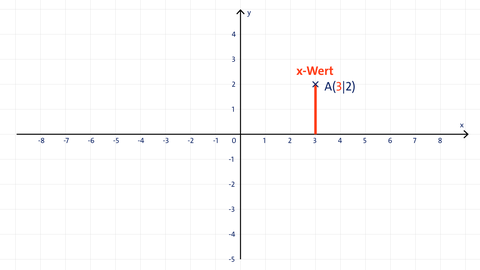
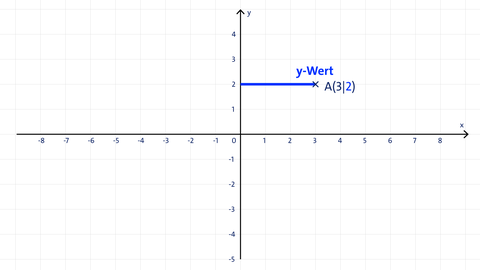
Vorgehensweise beim Eintrag des Punktes A(3|2) in das Koordinatensystem: Die Ziffer der x-Koordinate ist immer die 1. Stelle der Punktkoordinate, die y-Koordinaten die 2. Stelle, deshalb ist die x-Koordinate 3 und die y-Koordinate 2.
Die vier Quadranten im Koordinatensystem
Die vier Felder zwischen den Koordinatenachsen werden als Quadranten bezeichnet und werden gegen den Uhrzeigersinn mit den römischen Buchstaben I, II, III und IV gekennzeichnet.
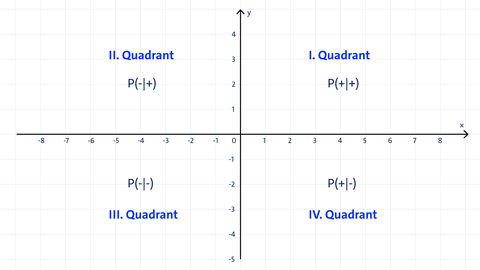
Punkte, die auf den Koordinatenachsen liegen, werden keinem Quadranten zugeordnet.
Beispielaufgabe: Punktkoordinaten im Koordinatensystem
Gegeben ist ein rechtwinkliges Koordinatensystem.
a) Zeichne den Punkt P(-3|-2) in das Koordinatensystem ein.
b) Gehe vom Punkt P(-3|-2) sechs Längeneinheiten nach rechts und vier Längeneinheiten nach oben und gib dann die Koordinaten des neuen Punktes Q an.
c) Erkläre, in welchen Quadranten die Punkte P und Q liegen.