Diese Folge beschäftigt sich mit verschiedenen Diagrammtypen. Du erfährst, wie diese Diagramme aufgebaut sind, wofür sie eingesetzt werden und wie du sie richtig interpretierst.
Diagrammtypen
Diagramme werden in der Statistik eingesetzt, um Daten anschaulich darzustellen. Dadurch lassen sie sich leichter verstehen, interpretieren und kommunizieren. Bei den Daten unterscheidet man zwischen nominalen und ordinalen Daten. Nominale Daten umfassen Kategorien ohne natürliche Reihenfolge, zum Beispiel Geschlecht (männlich, weiblich) oder Haarfarbe (blond, braun, schwarz). Ordinale Daten hingegen sind Kategorien, die eine natürliche Reihenfolge oder Rangfolge haben, wie zum Beispiel Schulnoten (1, 2, 3, 4, 5, 6) oder Zufriedenheitsgrade (sehr zufrieden, zufrieden, neutral, unzufrieden, sehr unzufrieden).
Punktdiagramm
Ein Punktdiagramm (auch Streudiagramm genannt und im Englischen als „scatter plot“ bekannt) ist ein grafisches Werkzeug zur Darstellung von Zusammenhängen zwischen zwei numerischen Variablen.
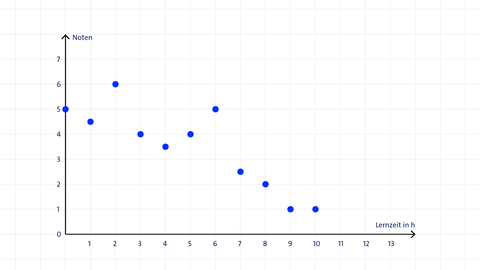
Beispiel: Zusammenhang zwischen der Lernzeit für eine Schulaufgabe (Zeit in Stunden) auf der horizontalen Achse und der erzielten Note (Noten zwischen 1 und 6) auf der vertikalen Achse.
Liniendiagramm
Ein Liniendiagramm (oder Kurvendiagramm) ist ein grafisches Werkzeug zur Darstellung von Datenpunkten, die durch Linien verbunden sind, typischerweise über einen bestimmten Zeitraum hinweg. Es zeigt, wie sich ein Wert im Zeitverlauf oder entlang einer geordneten Achse verändert. Die Punkte stehen für Messwerte, und die Linien verbinden diese der Reihenfolge nach, um einen Trend oder Verlauf sichtbar zu machen.
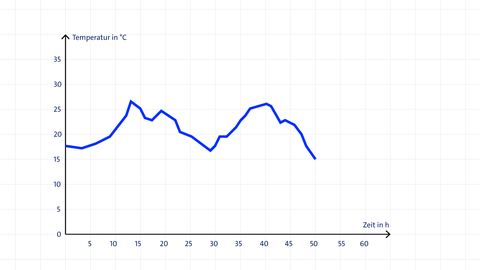
Beispiel: Temperatur im Wochenverlauf. Die Temperaturwerte werden im Diagramm als Punkte eingetragen und durch eine Linie verbunden – so erkennt man auf einen Blick den Temperaturverlauf über die Woche.
Stabdiagramm
Ein Stabdiagramm ist eine grafische Darstellung, die Häufigkeiten oder Werte einzelner Kategorien veranschaulicht. Dabei wird jede Kategorie durch einen einzelnen senkrechten oder waagrechten Strich, den sogenannten Stab, dargestellt. Das Diagramm verwendet Koordinatenachsen: Die waagerechte Achse zeigt die Merkmalsausprägungen, während die senkrechte Achse die Häufigkeiten angibt, entweder absolut oder relativ. Die Länge eines Stabs entspricht dabei der jeweiligen Häufigkeit.
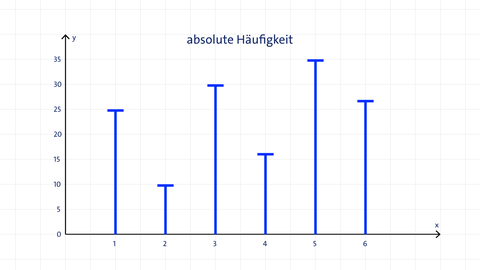
Beispiel: Häufigkeit von Mathematiknoten aller 11. Klassen der Schule. Im Stabdiagramm wird jede Note als dünner Strich dargestellt, die Höhe entspricht der Anzahl.
Säulendiagramm
Ein Säulendiagramm (im Englischen „column chart“) ist ein grafisches Werkzeug zur Darstellung von Daten in Form senkrechter Balken, den sogenannten Säulen. Es dient dazu, kategorische Daten miteinander zu vergleichen, beispielsweise Mengen, Häufigkeiten oder Werte. Ähnlich wie das Stabdiagramm besteht es aus rechteckigen Säulen, deren Höhe proportional zur dargestellten Datenmenge ist.
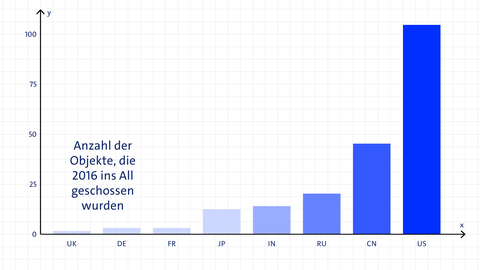
Beispiel: Anzahl der Objekte, die 2016 ins All geschossen worden. Die Säulen stehen für die beteiligten Länder, die Höhe zeigt die Anzahl der Objekte an.
Balkendiagramm
Ein Balkendiagramm ist ein grafisches Werkzeug zur Darstellung von Daten, bei dem horizontale Balken verwendet werden, um Werte oder Häufigkeiten verschiedener Kategorien zu vergleichen.
Anwendung von Balkendiagrammen
• Wenn die Kategorien lange Namen haben (horizontal besser lesbar).
• Wenn Häufigkeiten oder Werte verglichen werden.
• Wenn es viele Kategorien gibt. Beispiel: Anzahl der Objekte, die 2016 ins All geschossen worden. Die Säulen stehen für die beteiligten Länder, die Höhe zeigt die Anzahl der Objekte an.
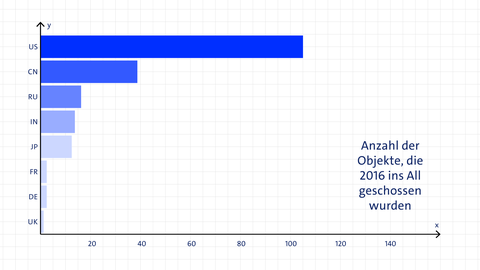
Beispiel: Anzahl der Objekte, die 2016 ins All geschossen worden. Die Balken stehen für die beteiligten Länder, die Länge zeigt die Anzahl der Objekte an.
Histogramm
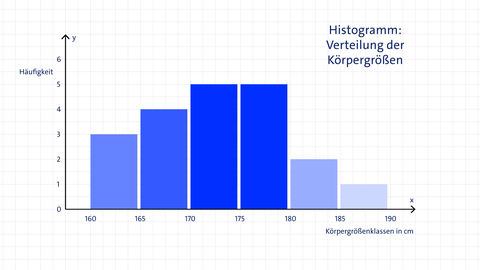
Ein Histogramm ist ein Diagramm zur Darstellung der Häufigkeitsverteilung von metrischen (numerischen) Daten; insbesondere bei großen Mengen kontinuierlicher Werte. Es zeigt, wie oft Werte in bestimmten Zahlenbereichen (Klassen oder Intervallen) vorkommen. Anders als bei einem Säulen- oder Balkendiagramm steht nicht jede einzelne Kategorie, sondern ein Zahlenintervall auf der x-Achse.
Anwendungsbeispiele:
• Verteilungen von Größen (Größe, Gewicht, Einkommen, Dauer, etc.)
• Erste Einschätzung der Form der Verteilung:
- symmetrisch
- schief (links oder rechts)
- bimodal (zwei Spitzen)
- Ausreißer erkennbar
Pareto-Diagramm
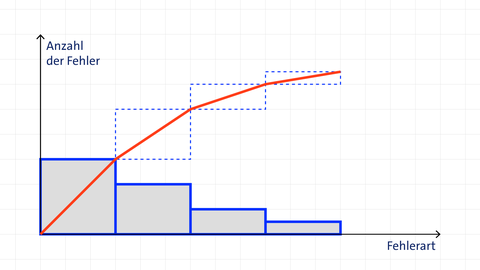
Ein Pareto-Diagramm ist ein spezielles Säulendiagramm, das auf dem Pareto-Prinzip (80/20-Regel) basiert. Es wird verwendet, um die wichtigsten Ursachen, Probleme oder Einflussfaktoren zu identifizieren, die den größten Effekt haben. Das Pareto-Prinzip (80/20-Regel) besagt, „80 % der Wirkung kommen von 20 % der Ursachen“. Das bedeutet, ein kleiner Teil der Probleme ist oft für den Großteil der Auswirkungen verantwortlich.
Anwendungsbeispiele:
• In der Qualitätskontrolle, Fehleranalyse oder Prozessoptimierung
• Um die wichtigsten Problemursachen zu erkennen
• Um gezielt Maßnahmen dort einzusetzen, wo sie am meisten bewirken
Boxplot
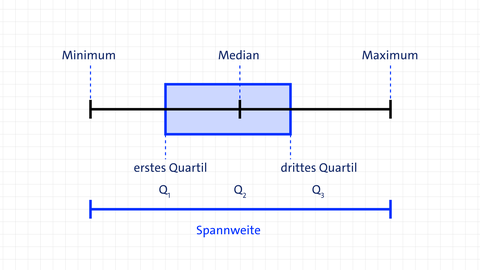
Ein Boxplot (Kastendiagramm) ist ein grafisches Werkzeug zur Darstellung der Verteilung eines metrischen Datensatzes.
Es zeigt auf einen Blick:
• Streuung (z. B. Spannweite, Quartile)
• Verteilung: Ist sie symmetrisch oder schief?
• Streuung: Wie weit sind die Daten gestreut?
• Zentralwert: Wo liegt der Median?
• Ausreißer: Gibt es ungewöhnlich hohe oder niedrige Werte?
Kreisdiagramm
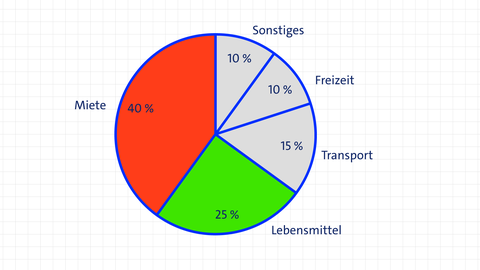
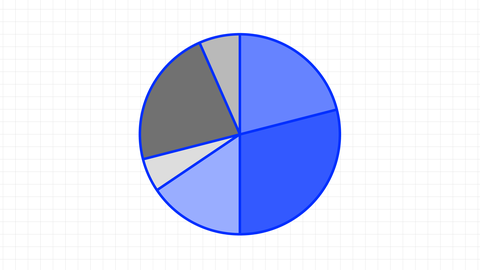
Ein Kreisdiagramm, auch Tortendiagramm genannt oder im Englischen als Pie Chart bekannt, ist ein kreisförmiges Diagramm, das verwendet wird, um Anteile eines Ganzen darzustellen. Jeder Abschnitt – jedes Tortenstück – repräsentiert eine Kategorie, und seine Größe entspricht dem prozentualen Anteil dieser Kategorie an der Gesamtheit.
Das Kreisdiagramm wird verwendet
• um Prozentsätze oder relative Häufigkeiten anschaulich zu machen
• um zu zeigen, welcher Teil wie viel zum Ganzen beiträgt
• in Präsentationen, Berichten, Infografiken (leicht verständlich)
Beispielaufgaben zu Diagrammen
Beispielaufgabe 1: Punkt- und Liniendiagramm
Deniz will wissen, ob es einen Zusammenhang gibt zwischen seinen Noten bei Klassenarbeiten und der Zeit, die er vor den Arbeiten jeweils ins Lernen investiert hat. Er notiert sich im ersten Schulhalbjahr also die Lernzeit in Stunden und die erzielten Notendurchschnitte:
| Lernzeit | 1 | 2 | 3 | 4 | 5 |
| Notendurchschnitt | 4,0 | 3,5 | 3,0 | 2,5 | 2,0 |
Wähle ein geeignetes Koordinatensystem und erstelle darin das Punkt- und das Liniendiagramm. Deute dann den Zusammenhang zwischen Lernzeit und Durchschnittsnoten.
Beispielaufgabe 2: Stabdiagramm
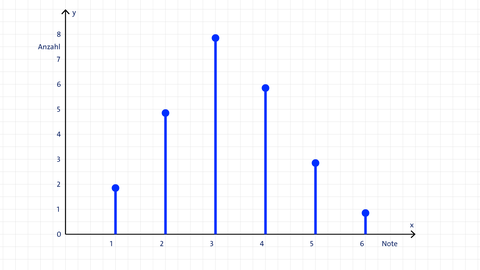
Das Diagramm zeigt, wie häufig eine Klassenarbeit jeweils mit den Noten "Sehr gut" (1) bis "Ungenügend" (6) bewertet wurden. Um welchen Typ von Diagramm handelt es sich hier?
Beispielaufgabe 3: Säulendiagramm
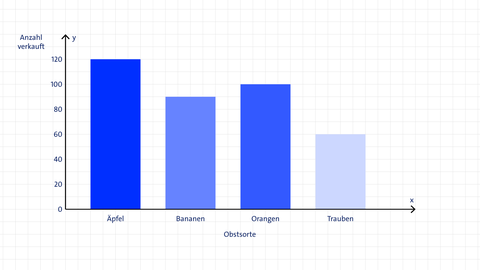
Lisa ist Auszubildende in der Obst- und Gemüseabteilung eines Supermarkts. Sie soll in einem Diagramm darstellen, wie oft bestimmte Obstsorten verkauft wurden. Interpretiere das Diagramm.
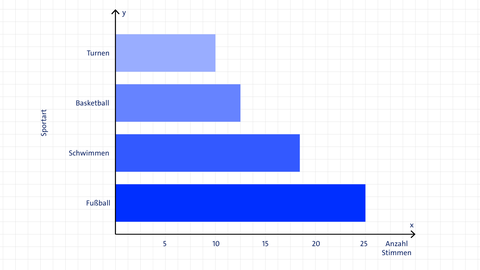
Beispielaufgabe 4: Balkendiagramm
Im örtlichen Turn- und Sportverein werden die Kinder befragt, welche Sportarten sie in diesem Jahr am liebsten machen wollen. Deute das Diagramm.
Beispielaufgabe 5: Pareto-Diagramm
Ein Versandunternehmen beschäftigt sich mit den Beschwerden und Reklamationen seiner Kunden. Die Ergebnisse liegen als geordnete Zahlen vor:
| Ursache | Lange Wartezeiten | Unfreundliches Personal | Falsche Rechnung | Schlechte Website |
| Häufigkeit | 40 | 30 | 20 | 10 |
Bewerte die Daten.
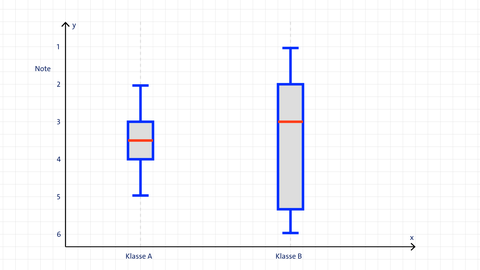
Beispielaufgabe 6: Boxplot
Ein Mathematiklehrer stellt die Prüfungsnoten seiner zwei Klassen in einem Boxplot dar. Analysiere die Daten.
Beispielaufgabe 7: Kreisdiagramm
Dein Mitbewohner stellt eure monatlichen Ausgaben in einem Diagramm dar. Beurteile das vorgelegte Diagramm.