In dieser Folge lernst du, wie allgemeine, gleichseitige, gleichschenklige und rechtwinkelige Dreiecke aussehen und wie man sie unterscheidet. Und du erfährst, wie Seitenlängen und Winkelgrößen berechnet werden.
Ein Dreieck ist eine flache geometrische Figur, die aus drei Seiten und drei Ecken besteht und ist die einfachste Polygonform. Das Dreieck wird durch die Verbindung von drei Punkten, den sogenannten Eckpunkten, die nicht auf einer geraden Linie liegen, gebildet. Die Seiten des Dreiecks sind die Strecken zwischen diesen Punkten.
Die Eigenschaften eines Dreiecks hängen von verschiedenen Faktoren ab, wie zum Beispiel den Längen der Seiten oder den Größen der Innenwinkel.
Beispielaufgabe: Dreiecksseitenberechnung
Das Dreieck ABC mit den Seitenlängen a = 12 m und b = 16 m hat einen Umfang U = 48 m. Ermittle die fehlende Seitenlänge c.
Beispielaufgabe: Winkelberechnung
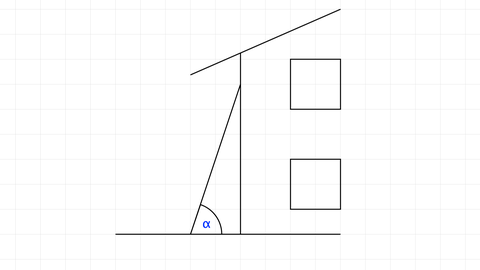
Eine Leiter lehnt an einer Hauswand. Der Winkel α zwischen Leiter und horizontalem Erdboden hat eine Größe von α= 72,5°. Bestimme den Winkel zwischen Leiter und Hauswand.
Geometrische Formen von Dreiecken
Einteilung der Dreiecke nach den Seitenlängen:
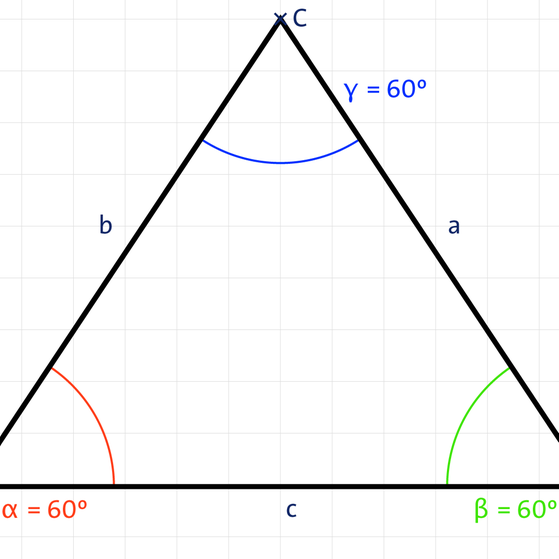
- Gleichseitiges Dreieck: Alle drei Seiten sind gleich lang.
- Gleichschenkliges Dreieck: Zwei Seiten sind gleich lang.
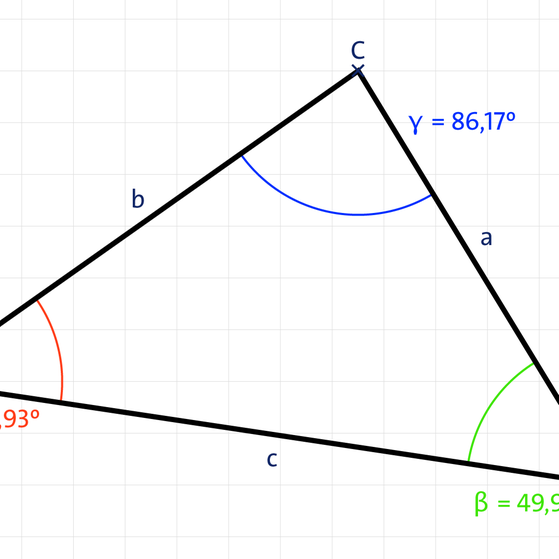
- Ungleichseitiges Dreieck: Alle drei Seiten haben unterschiedliche Längen.
Einteilung der Dreiecke nach den Innenwinkeln:
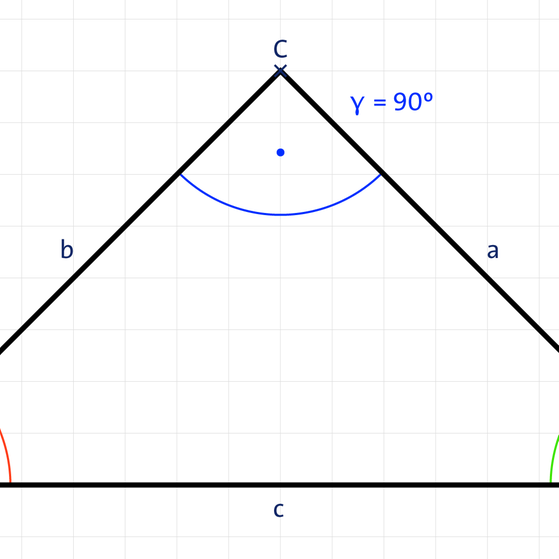
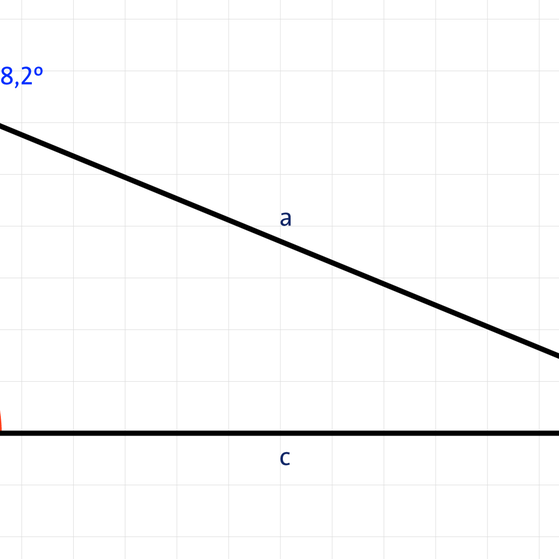
- Rechtwinkliges Dreieck: Ein Winkel ist genau 90° (rechter Winkel).
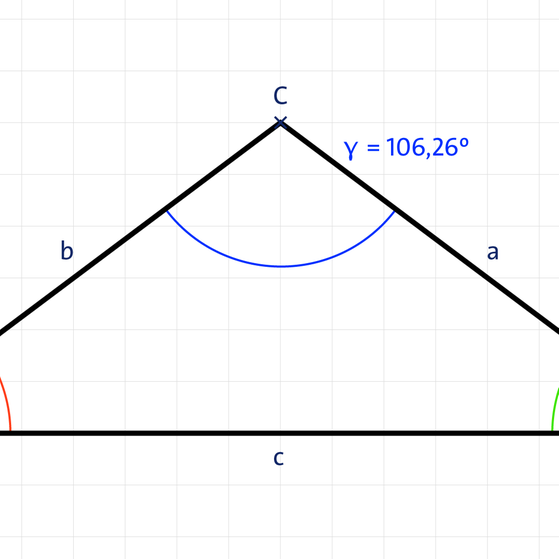
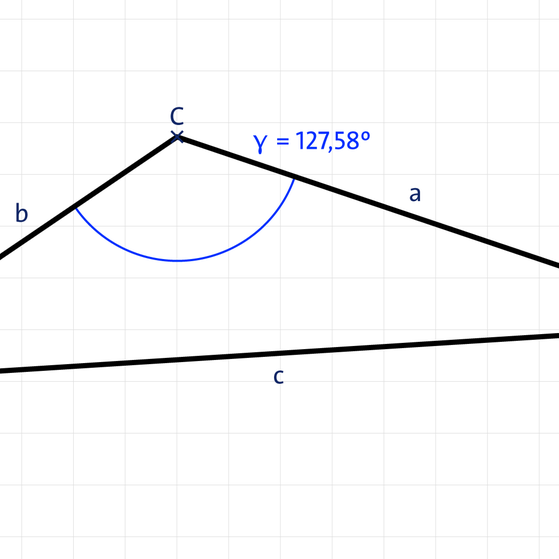
- Stumpfwinkliges Dreieck: Ein Winkel ist größer als 90°.
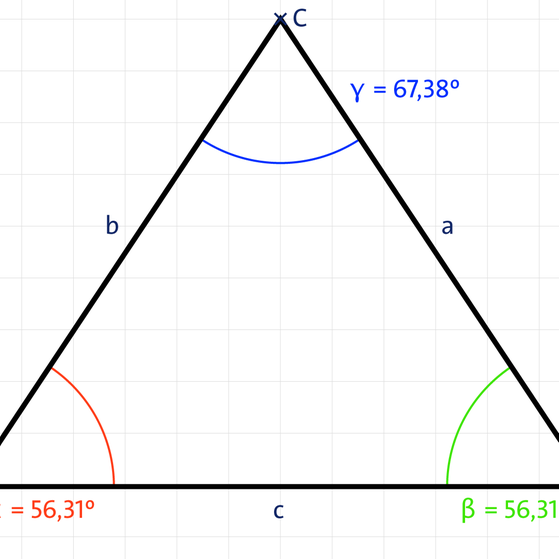
- Spitzwinkliges Dreieck: Alle Winkel sind kleiner als 90°.
Wichtige geometrische Eigenschaft aller Dreiecke
- Die Summe der Innenwinkel eines Dreiecks beträgt immer 180°.
- α + β + γ = 180°
- Umfang U: U = a + b + c